Hvem jukser?
Aktivitet
Forskere arbeider med å lage en ny test for å finne ut om idrettsutøvere bruker stoffet LiSTig. Dette stoffet er prestasjonsfremmende og er derfor forbudt.
Forskerne har samlet data som tyder på at testen fungerer bra, men de ser også at den noen ganger viser falske positive. Dermed kan testen si at en utøver har brukt LiSTig, selv om han ikke har gjort det. Testen viser også noen falske negative.
Hva er sjansen for at en idrettsutøver blir feilaktig anklaget for juks, eller at en juksemaker ikke blir avslørt?
Du kan undersøke dette spørsmålet med et praktisk eksperiment. Du trenger en mynt, en terning med fire blå sider og to røde sider, to vanlige terninger og noen røde, blå, grønne og gule multilink-kuber. Om du ikke har terninger med fargelagte sider, kan du bruke en vanlig terning og si at 1, 2, 3 og 4 er blå side og 5 og 6 er rød side.
Først ser vi på hva som skjer med en idrettsutøver.
Regler for simuleringen:
- Kast den fargelagte terningen.
- Blir det rødt, tar utøveren stoffet. Ta en rød kube.
- Blir det blått, tar ikke utøveren stoffet. Ta en blå kube.
- Dersom utøveren tar stoffet, kaster du to vanlige terninger.
- Dersom summen av terningene er 4, er utøverens test negativ. Ta en grønn kube.
- Alle andre summer betyr at utøverens test er positiv. Ta en gul kube.
- Dersom utøveren ikke tar stoffet, kaster du en mynt tre ganger.
- Dersom du får tre kron på rad, er utøverens test positiv. Ta en gul kube.
- Alle andre utfall betyr at utøverens test er negativ. Ta en grønn kube.
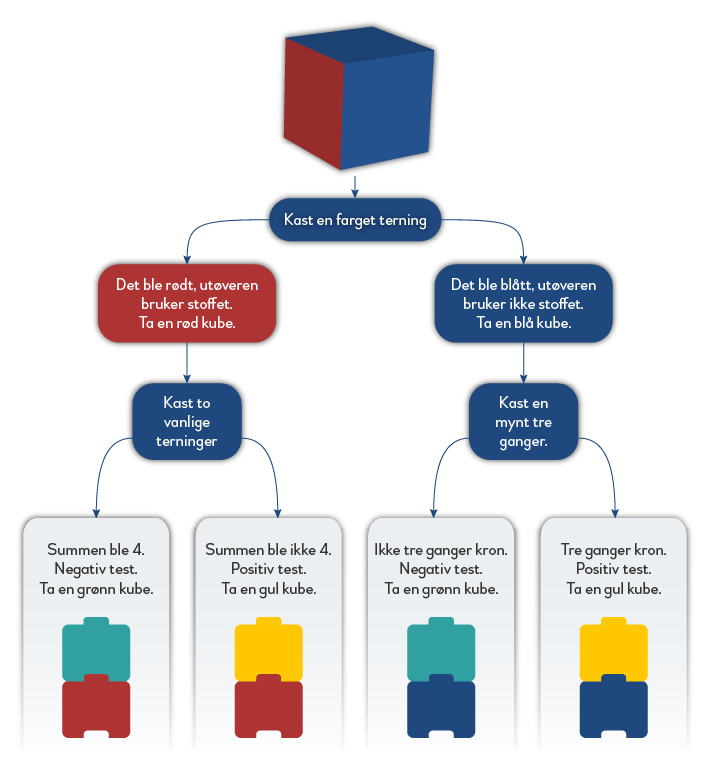
Simuleringen er oppsummert i dette flytskjemaet.
Sett sammen kubene du får for hver gjennomføring.
Hva betyr hver av kombinasjonene?
- rød og gul
- blå og gul
- rød og grønn
- blå og grønn
Gjenta eksperimentet slik at du har gjort det 36 ganger til sammen og sitter med 36 par kuber.
Blir du overrasket over resultatet?
Hvordan er resultatet sammenlignet med det vi kunne forvente? Kopioriginal 1 kan være til hjelp for å finne ut av dette spørsmålet.
Spørsmål å arbeide videre med
- Hva kan du si om andelen av falske positive (det vi si utøvere som får en positiv test, selv om de ikke har brukt stoffet)?
- Dersom en utøver ikke bruker stoffet, hva er sannsynligheten for at han får en positiv test?
- Hva kan du si om andelen av falske negative (det vil si utøvere som bruker stoffet, men likevel får en negativ test)?
- Dersom en utøver bruker stoffet, hva er sannsynligheten for at testen er negativ? Hvilket tall bør det være i nevneren her?
Kopioriginal 2 kan hjelpe deg med å tolke den forventede fordelingen som sannsynligheter, og leder deg mot en generell regel som du kan bruke blant annet i valgtre – multiplikasjonsregelen.
Enda flere spørsmål å arbeide videre med
Når du arbeider med disse spørsmålene, er det viktig at du har klart for deg hvilke utøvere det er snakk om, slik at du vet hvilket tall som skal i nevneren for sannsynligheten. Det er ikke alltid det samme.
- Hva er sannsynligheten for at en tilfeldig utøver får et falskt positivt resultat?
- Hva er sannsynligheten for at en utøvers testresultat er positivt, selv om han ikke har brukt stoffet?
- Hva er sannsynligheten for at en utøver ikke har brukt stoffet, selv om han får et positivt testresultat?
Hvilken representasjon er mest hensiktsmessig for å besvare disse spørsmålene, og hvorfor?
Lærerveiledning
Hvorfor arbeide med denne oppgaven?
Denne oppgaven modellerer tolkningen av statistikk for testing av for eksempel kreft, HIV, graviditet, DNA og mange andre lignende situasjoner, også dopingtester.
En teoretisk tilnærming til sannsynlighet er ofte vanskelig for mange elever på lavere trinn. Tilnærmingen i oppgaven kan hjelpe dem til å få en strukturert forståelse av spørsmålene, som kan besvares med hjelp av valgtre og tabeller, som leder mot multiplikasjonsregelen. I tillegg vil de bli mer oppmerksomme på at de må være nøye med hvilket delsett av datamaterialet som gir nevneren i sannsynligheten.
Elever som ønsker å gå videre, kan også bruke oppgaven til å vurdere forskjellen mellom P(A|B) og P(B|A), og de kan introduseres for Bayes teorem.
Mulig tilnærming
Del elevene i grupper på 3–4, og la dem få nok utstyr til å gjennomføre eksperimentet 36 ganger. Det kan være lurt at de gjør eksperimentet med terninger og kuber, og at dere har en innledende diskusjon før du deler ut kopioriginaler.
Gjennomfør eksperimentet i plenum med én elev (flere om det trengs) for å vise hvordan metoden fungerer. Deretter skal elevene samle egne data og sette sammen 36 par med multikuber.
Når alle har samlet data, må de skrive resultatene sine i valgtreet og tabellen i kopioriginal 1.
Så kan de arbeide med spørsmålene i oppgaven og i kopioriginal 2.
Gode veiledningsspørsmål
Begynn med spørsmål om de faktiske resultatene. Her er noen av spørsmålene du kan stille:
- Er du overrasket over resultatet?
- Hva tenker du om denne testen, og hvor effektiv er den?
- Hva kan du si om andelen av falske positive?
- Hva er sannsynligheten for at en utøver tester positivt, selv om han ikke har brukt stoffet?
- Hva kan du si om andelen av falske negative?
- Hva er sannsynligheten for at en utøver tester negativt, selv om han har brukt stoffet?
Mulig utvidelse
Spørsmål for videre arbeid finner du på oppgavesiden og i kopioriginalene. De gir elevene mulighet til å finne sannsynligheter på formen P(A|B) og P(B|A) og til å belyse forskjellen mellom dem.
Utvidelsesspørsmålene «Enda flere spørsmål å arbeide videre med» handler om det samme settet med tre utøvere som ikke bruker stoffet, men likevel får positive tester. Telleren i hvert spørsmål er derfor 3. Men nevneren er ulik i de forskjellige spørsmålene, siden vi sammenligner de tre utøverne med andre sett av utøvere.
Elevene bør oppfordres til å kritisere modellen. Hvilke forutsetninger bygger den på? Hvordan kan du forbedre den for å gjøre den mer realistisk?
Ressursen er utviklet av NRICH