Kven juksar?
Aktivitet
Forskarar arbeider med å lage ein ny test for å finne ut om idrettsutøvarar brukar stoffet LiSTig. Dette stoffet er prestasjonsfremjande og er difor forbode.
Forskarane har samla data som tyder på at testen fungerer bra, men dei ser også at han av og til viser falske positive. Dermed kan testen seie at ein utøvar har brukt LiSTig, sjølv om han ikkje har gjort det. Testen viser også nokre falske negative.
Kva er sjansen for at ein idrettsutøvar blir feilaktig skulda for juks, eller at ein juksemakar ikkje blir avslørt?
Du kan undersøkje dette spørsmålet med eit praktisk eksperiment. Du treng ein mynt, ein terning med fire blå sider og to raude sider, to vanlege terningar og nokre raude, blå, grøne og gule multilink-kubar. Om du ikkje har terningar med fargelagde sider, kan du bruke ein vanleg terning og seie at 1, 2, 3 og 4 er blå sider og 5 og 6 er raude sider.
Først ser vi på det som skjer med ein idrettsutøvar.
Reglar for simuleringa:
- Kast den fargelagde terningen.
- Blir det raudt, tek utøvaren stoffet. Ta ein raud kube.
- Blir det blir blått, tek ikkje utøvaren stoffet. Ta ein blå kube.
- Dersom utøvaren tek stoffet, kastar du to vanlege terningar.
- Dersom summen av terningane er 4, er testen til utøvaren negativ. Ta ein grøn kube.
- Alle andre summar betyr at testen til utøvaren er positiv. Ta ein gul kube.
- Dersom utøvaren ikkje tek stoffet, kastar du ein mynt tre gonger.
- Får du tre kron på rad, er testen til utøvaren positiv. Ta ein gul kube.
- Alle andre utfall betyr at testen til utøvaren er negativ. Ta ein grøn kube.
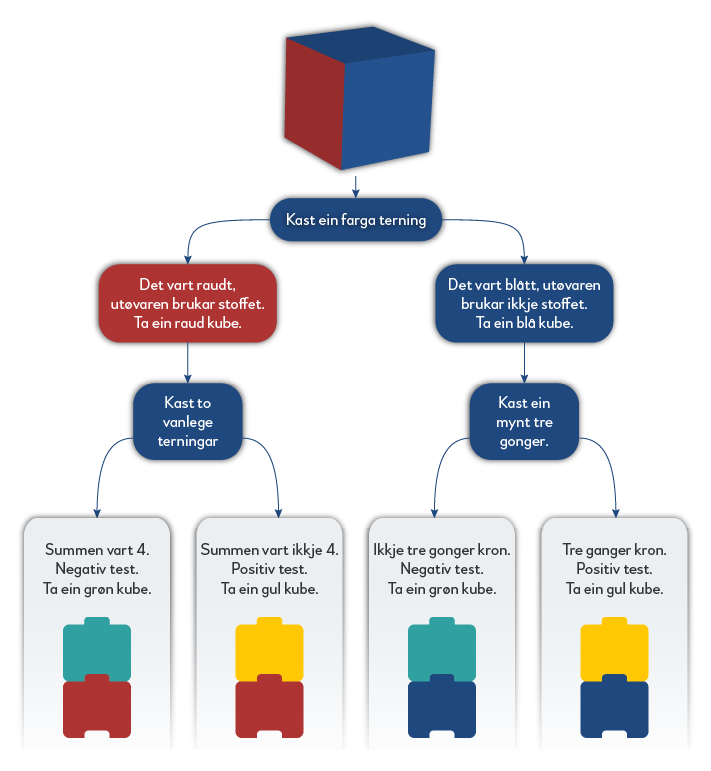
Simuleringa er summert opp i dette flytskjemaet.
Set saman kubane du får for kvar gjennomføring.
Kva betyr kvar av kombinasjonane?
- raud og gul
- blå og gul
- raud og grøn
- blå og grøn
Gjenta eksperimentet slik at du har gjort det 36 gonger til saman og sit med 36 par kubar.
Blir du overraska over resultatet?
Korleis er resultatet samanlikna med det vi kunne vente? Kopioriginal 1 kan vere til hjelp for å finne ut av dette spørsmålet.
Spørsmål å arbeide vidare med
- Kva kan du seie om andelen av falske positive (det vi seie utøvarar som får ein positiv test, sjølv om dei ikkje har brukt stoffet)?
- Dersom ein utøvar ikkje brukar stoffet, kva er sannsynet for at han får ein positiv test?
- Kva kan du seie om andelen av falske negative (det vil seie utøvarar som brukar stoffet, men likevel får ein negativ test)?
- Dersom ein utøvar brukar stoffet, kva er sannsynet for at testen er negativ? Kva for eit tal bør det vere i nemnaren her?
Kopioriginal 2 kan hjelpe deg med å tolke den venta fordelinga som sannsyn, og leier deg mot ein generell regel som du kan bruke mellom anna i valtre – multiplikasjonsregelen.
Endå fleire spørsmål å arbeide vidare med
Når du arbeider med desse spørsmåla, er det viktig at du har klart for deg kva for utøvarar det er snakk om, slik at du veit kva for eit tal som skal i nemnaren for sannsynet. Det er ikkje alltid det same.
- Kva er sannsynet for at ein tilfeldig utøvar får eit falskt positivt resultat?
- Kva er sannsynet for at testresultatet til ein utøvar er positivt, sjølv om han ikkje har brukt stoffet?
- Kva er sannsynet for at ein utøvar ikkje har brukt stoffet, sjølv om han får eit positivt testresultat?
Kva representasjon er mest tenleg for å svare desse spørsmåla, og kvifor?
Lærarrettleiing
Kvifor arbeide med denne oppgåva?
Denne oppgåva modellerer tolkinga av statistikk for testing av for eksempel kreft, HIV, graviditet, DNA og mange andre liknande situasjonar, også dopingtestar.
Ei teoretisk tilnærming til sannsyn er ofte vanskeleg for mange elevar på lågare trinn. Tilnærminga i oppgåva kan hjelpe dei til å få ei strukturert forståing av spørsmåla, som dei kan svare på med hjelp av valtre og tabellar, som leier mot multiplikasjonsregelen. I tillegg vil dei bli meir merksame på at dei må vere nøye med kva for eit delsett av datamaterialet som gir nemnaren i sannsynet.
Elevar som ønskjer å gå vidare, kan også bruke oppgåva til å vurdere skilnaden mellom P(A|B) og P(B|A), og dei kan introduserast for Bayes teorem.
Mogleg tilnærming
Del elevane i grupper på 3–4, og la dei få nok utstyr til å gjennomføre eksperimentet 36 gonger. Det kan vere lurt at dei gjer eksperimentet med terningar og kubar, og at de har ein innleiande diskusjon før du deler ut kopioriginalar.
Gjer eksperimentet i plenum med éin elev (fleire om det trengst) for å vise korleis metoden fungerer. Deretter skal elevane samle eigne data og setje saman 36 par med multikubar.
Når alle har samla data, må dei skrive resultata sine i valtreet og tabellen i kopioriginal 1.
Så kan dei arbeide med spørsmåla i oppgåva og i kopioriginal 2.
Gode rettleiingsspørsmål
Begynn med spørsmål om dei faktiske resultata. Her er nokre av spørsmåla som kan stillast:
- Er du overraska over resultatet?
- Kva tenkjer du om denne testen, og kor effektiv er han?
- Kva kan du seie om andelen av falske positive?
- Kva er sannsynet for at ein utøvar testar positivt, sjølv om han ikkje har brukt stoffet?
- Kva kan du seie om andelen av falske negative?
- Kva er sannsynet for at ein utøvar testar negativt, sjølv om han har brukt stoffet?
Mogleg utviding
Spørsmål for vidare arbeid finn du på oppgåvesida og i kopioriginalane. Dei gjer det mogleg for elevane å finne sannsyn på forma P(A|B) og P(B|A), og å sjå nærare på skilnaden mellom dei.
Utvidingsspørsmåla «Endå fleire spørsmål å arbeide vidare med» handlar om det same settet med tre utøvarar som ikkje brukar stoffet, men likevel får positive tester. Teljaren i kvart spørsmål er difor 3. Men nemnaren er ulik i dei forskjellige spørsmåla, sidan vi samanliknar dei tre utøvarane med andre sett av utøvarar.
Elevane bør oppfordrast til å kritisere modellen. Kva for føresetnader byggjer han på? Korleis kan du forbetre han for å gjere han meir realistisk?
Ressursen er utviklet av NRICH