Paraboler, igjen
Aktivitet
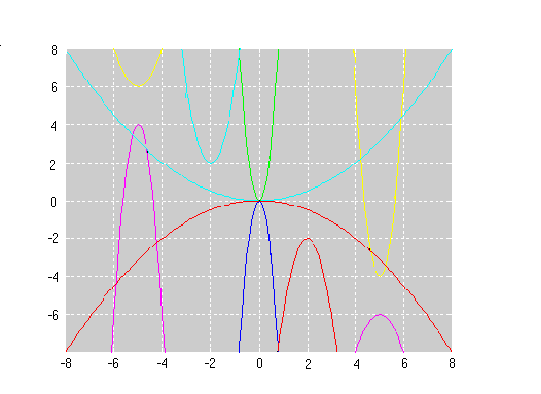
Nedenfor ser du et mønster som du kan eksperimentere med. Det er satt sammen av 14 andregradsfunksjoner. Du kan bruke en graftegner, for eksempel GeoGebra, når du arbeider med denne oppgaven.
Funksjonsuttrykkene til tre av grafene:
\(y=2(x-6)^2-4\\ y=2x^2-1\\ y=-2(x-4)^2+3 \)
Finn funksjonsuttrykkene til de 11 andre grafene i mønsteret.
Starthjelp
Prøv å finne ut hva som endres når grafen til \(y=x^2\) transformeres til grafene til \(y=ax^2\), \(y=(x+b)^2\) og \(y=x^2+c\), ved å eksperimentere med forskjellige verdier for a, b og c. Prøv med små tallverdier, både positive og negative.
Lærerveiledning
Hvorfor arbeide med denne oppgaven?
I stedet for at elevene skal få forskjellige funksjonsuttrykk og tegne grafene, skal de i denne oppgaven finne funksjonsuttrykkene til forskjellige grafer Det kan oppmuntre dem til å eksperimentere med å endre funksjonsuttrykkene systematisk for å oppdage hvilken effekt endringene har på grafene. Denne oppgaven legger til rette for arbeid med funksjoner, på samme måte som Parabolmønster.
Mulig utvidelse
Elevene kan prøve å finne funksjonsuttrykkene til grafene i mønsteret nedenfor.
Ressursen er utviklet av NRICH