Parabolar, igjen
Aktivitet
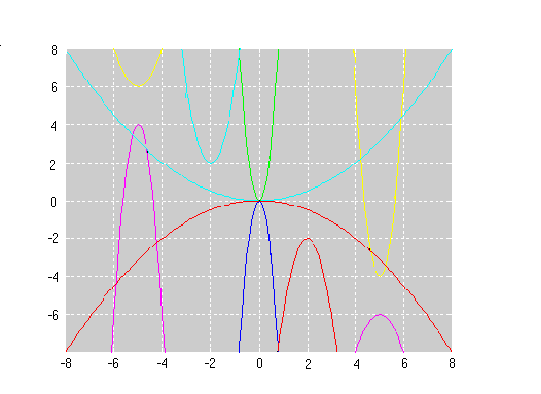
Nedanfor ser du eit mønster som du kan eksperimentere med. Det er sett saman av 14 andregradsfunksjonar. Du kan bruke ein grafteiknar, for eksempel GeoGebra, når du arbeider med denne oppgåva.
Funksjonsuttrykka til tre av grafane:
\(y=2(x-6)^2-4\\ y=2x^2-1\\ y=-2(x-4)^2+3 \)
Finn funksjonsuttrykka til dei 11 andre grafane i mønsteret.
Starthjelp
Prøv å finne ut kva som endrar seg når grafen til \(y=x^2\) blir transformert til grafane til \(y=ax^2\), \(y=(x+b)^2\) og \(y=x^2+c\), ved å eksperimentere med forskjellige verdiar for a, b og c. Prøv med små talverdiar, både positive og negative.
Lærarrettleiing
Kvifor arbeide med denne oppgåva?
I staden for at elevane skal få forskjellige funksjonsuttrykk og teikne grafane, skal dei i denne oppgåva finne funksjonsuttrykka til forskjellige grafar. Det kan oppmuntre dei til å eksperimentere med å endre funksjonsuttrykka systematisk for å oppdage kva effekt endringane har på grafane. Denne oppgåva legg til rette for arbeid med funksjonar, på same måten som Parabolmønster.
Mogleg utviding
Elevane kan prøve å finne funksjonsuttrykka til grafane i mønsteret nedanfor.
Ressursen er utviklet av NRICH