Parabolmønster
Aktivitet
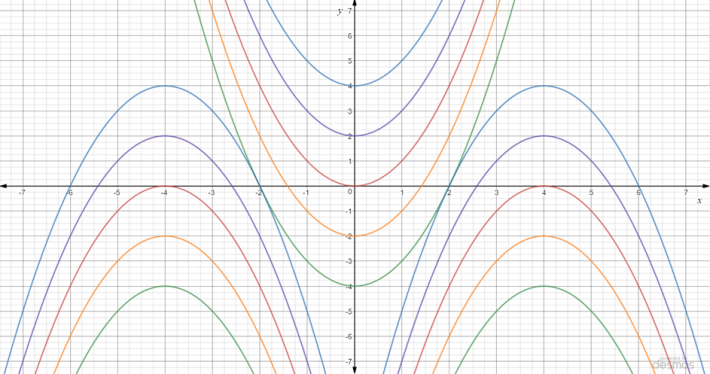
På biletet nedanfor ser du grafen til ei gruppe med 15 funksjonar. To av dei har likningane: \(y=x^2\\ y=-(x-4)^2\)
Kan du finne funksjonsuttrykka til dei andre grafane på biletet?
Du kan bruke ein grafteiknar, for eksempel GeoGebra, til å skape det same mønsteret.
Kan du finne funksjonsuttrykka til desse grafane?
Starthjelp
- Prøv å teikne grafen til \(y=x^2\) på papir. Korleis ventar du at grafen til \(y=-x^2\) vil sjå ut? Kva effekt har minusteiknet? Er denne grafen med på biletet i oppgåva?
- Korleis ventar du at grafen til \(y=(x-4)^2\) vil sjå ut? Korleis ventar du at grafen til \(y=x^2\) vil bli transformert for å gi grafen til \(y=(x-4)^2\)?
- Korleis blir grafen til \(y=-(x-4)^2\)?
- Bruk ein grafteiknar, og teikn grafane til funksjonane. Stemmer dei med det du såg for deg?
- Kva har du lært i dette eksempelet om refleksjonar og forskyvingar av grafar, og funksjonsuttrykka som høyrer til?
- Eksperimenter med å teikne grafane til andre funksjonar, og sjå om du kan finne funksjonsuttrykka til alle grafane på biletet.
Lærarrettleiing
Kvifor arbeide med denne oppgåva?
I staden for at elevane skal få forskjellige funksjonsuttrykk og teikne grafane, skal dei i denne oppgåva finne funksjonsuttrykka til dei forskjellige grafane. Det kan oppmuntre dei til å eksperimentere med å endre funksjonsuttrykka systematisk for å oppdage effekten som endringane har på grafane.
Mogleg tilnærming
Det kan vere nyttig å dele ut Kopioriginal 1.
Begynn med å vise det første biletet. La elevane samarbeide i par for å finne grafane til \(y=x^2\) og \(y=-(x-4)^2\).
Be elevane om å gjere greie for likskapar og ulikskapar mellom dei to grafane. Utfordringa deira blir å lage heile mønsteret på nytt ved hjelp av ein grafteiknar, for eksempel GeoGebra. Dei må finne ut korleis endringar i funksjonsuttrykka påverkar forma og plasseringa til grafane.
Gi elevane god tid til å eksperimentere med grafteiknaren. Etter ei stund bør klassen ha ein diskusjon i plenum, der elevane får dele nyttige observasjonar dei har gjort. Nokre eksempel på observasjonar som dei kan gjere:
- \(y=-x^2\) er det same som \(y=x^2\), men snudd opp ned.
- \(y=x^2+4\) er det same som \(y=x^2\), men flytt 4 einingar opp.
- \(y=(x-3)^2\) er det same som \(y=x^2\), men flytt 3 einingar til høgre.
Når elevane har delt observasjonane sine, bør dei få tid til å bruke innspela frå andre til å fullføre oppgåva. Deretter kan dei lage eigne mønster ved å bruke andregradsfunksjonar.
Til slutt kan dei skrive ut eller dele mønstera sine med andre grupper på anna vis, og utfordre dei til å finne funksjonsuttrykka som vart nytta for å lage mønsteret.
Gode rettleiingsspørsmål
- Du blir beden om å finne funksjonsuttrykka til ei gruppe funksjonar. Kvifor kan vi kalle dei ei gruppe funksjonar?
- Kva er likt og kva er ulikt med funksjonsuttrykka \(y=x^2\) og \(y=-(x-4)^2\)?
- Korleis kan desse likskapane og ulikskapane ha samanheng med korleis grafane ser ut, og kvar dei er plasserte i forhold til aksane?
- Kan du forklare kvifor reglane du har funne, vil fungere på grafane til andre funksjonar?
Mogleg utviding
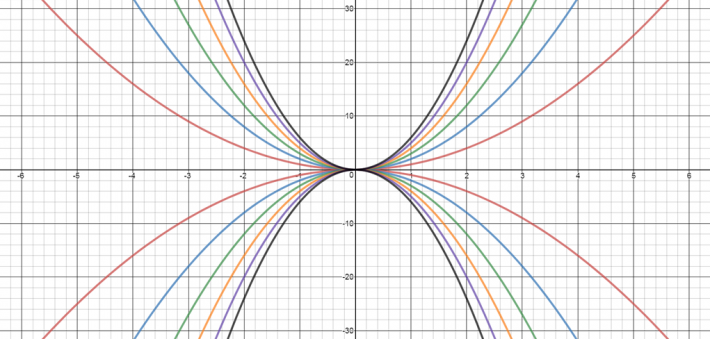
- Kopioriginal 2 inneheld eit anna sett med grafar som elevane kan identifisere. Dei kan også fokusere på krumming.
- Parabolar – igjen inneheld liknande bilete som skal lagast på nytt.
- Utforske kubiske funksjonar brukar grafane til kubiske funksjonar på liknande måte.
Ressursen er utviklet av NRICH