Læreplankoblet

LAST NED kopioriginaler

Parabolmønster

Stikkord: Funksjoner Andregradsfunksjoner

Aktivitet

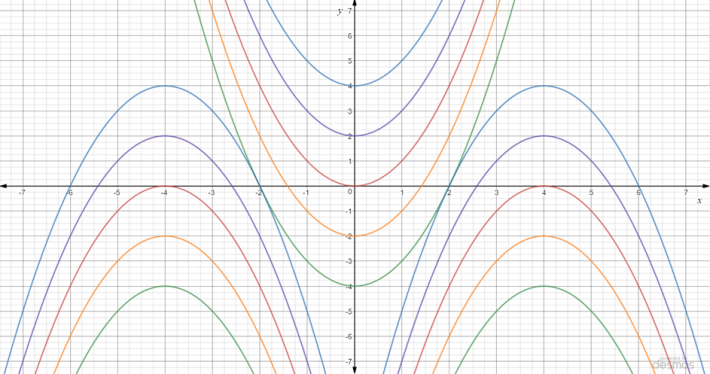
På bildet nedenfor ser du grafen til en gruppe med 15 funksjoner. To av dem har likningene: \(y=x^2\\ y=-(x-4)^2\)

Grafene til 15 andregradsfunksjoner.

Kan du finne funksjonsuttrykkene til de andre grafene på bildet?
Du kan bruke en graftegner, for eksempel GeoGebra, til å gjenskape mønsteret.

Kan du finne funksjonsuttrykkene til disse grafene?

Grafene til 12 andregradsfunksjoner.

Starthjelp

  • Prøv å tegne grafen til \(y=x^2\) på papir. Hvordan forventer du at grafen til \(y=-x^2\) vil se ut? Hvilken effekt har minustegnet? Er denne grafen med på bildet i oppgaven?
  • Hvordan vil du forvente at grafen til \(y=(x-4)^2\) ser ut? Hvordan forventer du at grafen til \(y=x^2\) vil bli transformert for å gi grafen til \(y=(x-4)^2\)?
  • Hvordan blir grafen til \(y=-(x-4)^2\)?
  • Bruk en graftegner og tegn grafene til funksjonene. Stemmer de med forventningene dine?
  • Hva har du lært i dette eksemplet om refleksjoner og forskyvninger av grafer og de tilhørende funksjonsuttrykkene?
  • Eksperimenter med å tegne grafene til andre funksjoner, og se om du kan finne funksjonsuttrykkene til alle grafene på bildet.

Lærerveiledning

Hvorfor arbeide med denne oppgaven?

I stedet for at elevene skal få forskjellige funksjonsuttrykk og tegne grafene, skal de i denne oppgaven finne funksjonsuttrykkene til de forskjellige grafene. Det kan oppmuntre dem til å eksperimentere med å endre funksjonsuttrykkene systematisk for å oppdage hvilken effekt endringene har på grafene.

Mulig tilnærming

Det kan være hensiktsmessig å dele ut Kopioriginal 1.

Begynn med å vise det første bildet. La elevene samarbeide i par for å finne grafene til \(y=x^2\) og \(y=-(x-4)^2\).

Be elevene om å beskrive hva som er likheter og ulikheter mellom de to grafene. Utfordringen deres blir å gjenskape hele mønsteret ved hjelp av en graftegner, for eksempel GeoGebra. De må finne ut hvordan endringer i funksjonsuttrykkene påvirker formen og plasseringen til grafene.

Gi elevene god tid til å eksperimentere med graftegneren. Etter en stund bør klassen ha en diskusjon i plenum, der elevene får dele nyttige observasjoner de har gjort. Noen eksempler på observasjoner som de kan gjøre:

  • \(y=-x^2\) er det samme som \(y=x^2\), men snudd opp ned.
  • \(y=x^2+4\) er det samme som \(y=x^2\), men flyttet opp 4 enheter.
  • \(y=(x-3)^2\) er det samme som \(y=x^2\), men flyttet 3 enheter til høyre.

Når elevene har delt observasjonene sine, bør de få tid til å bruke andres innspill til å fullføre oppgaven. Deretter kan de lage egne mønstre ved å bruke andregradsfunksjoner.

Avslutningsvis kan de skrive ut eller dele mønstrene sine med andre grupper på annet vis, og utfordre dem til å finne funksjonsuttrykkene som ble brukt for å lage mønsteret.

Gode veiledningsspørsmål

  • Du blir bedt om å finne funksjonsuttrykkene til en gruppe funksjoner. Hvorfor kan vi kalle dem en gruppe funksjoner?
  • Hva er likt og hva er ulikt med funksjonsuttrykkene \(y=x^2\) og \(y=-(x-4)^2\)?
  • Hvordan kan disse likhetene og ulikhetene ha sammenheng med hvordan grafene ser ut, og hvor de er plassert i forhold til aksene?
  • Kan du forklare hvorfor reglene du har funnet, vil fungere på grafene til andre funksjoner?

Mulig utvidelse

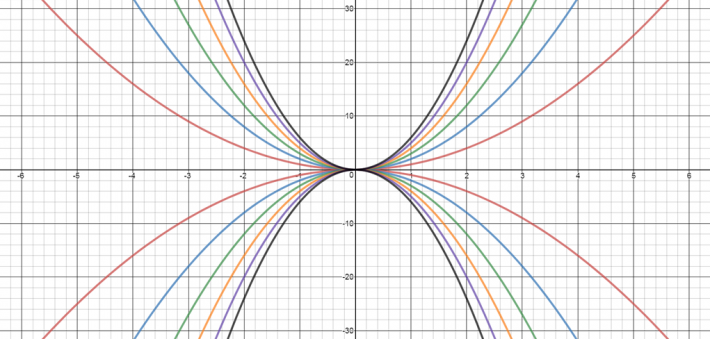
  • Kopioriginal 2 inneholder et annet sett med grafer som elevene kan identifisere. De kan også fokusere på krumming.
  • Paraboler – igjen inneholder lignende bilder som skal gjenskapes.
  • Utforske kubiske funksjoner bruker grafene til kubiske funksjoner på lignende måte.

Ressursen er utviklet av NRICH

9,10