Læreplankoblet

Spill til 37

Stikkord: Addisjon Strategisk tenking Systematisering

Aktivitet

Thumbnail

Dette er et spill for to spillere.

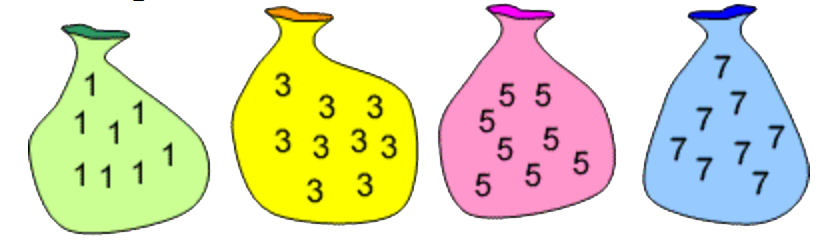
Hver pose har et ubegrenset antall av tallene 1, 3, 5 og 7.

Spilleregler:

  1. Bestem hvem som skal begynne.

  2. Spiller 1 velger ett av tallene fra posene over (1, 3, 5 eller 7).

  3. Spiller 2 velger deretter et tall fra en av posene, og legger det sammen med det forrige tallet.

  4. Spiller 1 velger et tall fra posene og legger det til forrige totalsum.

  5. Spillet fortsetter slik, og vinneren av spillet er den spilleren som legger til det siste tallet som gjør at summen blir 37.

Starthjelp

  • Hvor mange tall har dere brukt i alt i spillet?

  • Prøv igjen. Hvor mange tall brukte dere denne gangen?

  • Hva er det største antallet tall dere kan bruke for å nå 37?

  • Hva er det minste antallet tall dere kan bruke for å nå 37?

  • Kan dere bruke alle antall tall mellom det minste og det størst mulige for å nå 37?

  • Hva legger dere merke til? Kan dere forklare? 

Frida sier: «Jeg må velge først for å vinne!» Er dere enige med Frida? Hvorfor eller hvorfor ikke?

Løsning

Det minste antallet tall som kan brukes, er 7 (for eksempel 7 + 7 + 7 + 7 + 7 + 1 + 1).

Det største antallet tall som kan brukes, er 37 (37 1-tall).

Mulige antall tall (eller trekk) vil alltid være et oddetall. Grunnen til det er at oddetall + oddetall gir partall, og hvis man legger sammen et partall av tall som er oddetalltall,  vil summen bli et partall (og dermed ikke 37). Her er løsningene som noen elever har listet opp:

Eksempel på kombinasjon  Antall trekk 
\((5\cdot7)+(2\cdot1)=37\) \(7\)
\((4\cdot7)+(4\cdot1)+5=37\) \(9\)
\((3\cdot7)+(6\cdot1)+(2\cdot5)=37\) \(11\)
\((2\cdot7)+(8\cdot1)+(3\cdot5)=37\) \(13\)
\((1\cdot7)+(10\cdot1)+(4\cdot5)=37\) \(15\)
\((5\cdot3)+(2\cdot5)+(12\cdot1)=37\) \(17\)
\((6\cdot3)+(1\cdot7)+(12\cdot1)=37\) \(19\)
\((4\cdot3)+(2\cdot5)+(15\cdot1)=37\) \(21\)
\((3\cdot3)+(2\cdot5)+(18\cdot1)=37\) \(23\)
\((2\cdot3)+(2\cdot5)+(21\cdot1)=37\) \(25\)
\((1\cdot3)+(2\cdot5)+(24\cdot1)=37\) \(27\)
\((2\cdot5)+(27\cdot1)=37\) \(29\)
\((1\cdot7)+(30\cdot1)=37\) \(31\)
\((1\cdot5)+(32\cdot1)=37\) \(33\)
\((1\cdot3)+(34\cdot1)=37\) \(35\)
\(37\cdot1=37\) \(37\)

Spilleren som begynner, vinner alltid. Spiller 1 velger et oddetall. Spiller 2 velger også et oddetall, og da blir summen et partall. Spiller 1 velger igjen et oddetall, og summen blir et oddetall. Slik fortsetter det.

Spiller 1: oddetall

Spiller 2: oddetall + oddetall gir partall

Spiller 1: partall + oddetall gir oddetall

....

37 er et oddetall, så summen til spiller 2 vil aldri bli 37. Dermed er det alltid spiller 1 som vinner.

Lærerveiledning

Hvorfor arbeide med denne oppgaven?

På det enkleste gir denne oppgaven elevene mulighet til å øve seg på addisjon. Men for å vinne spillet må elevene begynne å tenke strategisk, og det er mye mer utfordrende. Det å analysere antallet tall som brukes, gir enda en utfordring, og elevene får mulighet til å generalisere egenskaper ved addisjon med oddetall.

Mulig tilnærming

Vis bildet med posene på tavla, og forklar reglene for spillet. Du kan foreslå at du spiller mot klassen, eller du kan dele klassen inn i to lag som skalspille mot hverandre. Bruk uansett tavla til å holde oversikt over tallene som blir brukt, og totalsummen. Spill en gang til på samme måte, og skriv  tallene og totalsummene på tavla.

Gi elevene tid til å spille flere ganger i par, og be dem om å notere tall og summer mens de spiller. Samle deretter klassen igjen, og spør hvert par hvor mange tall de brukte i hver runde. Noter dette på tavla. Pek på det største og det minste tallet, og spør elevene om de tror at dette er det største og det minste mulige antallet tall som kan brukes. Utfordre dem til å finne ut av dette, og deretter til å finne ut av alle mulige antall mellom det største og det minste.

I plenum kan du skrive opp alle antall tall som er brukt, fra 7 (7 + 7 + 7 + 7 + 7 + 1 + 1) til 37 (37 1-tall). Hva legger klassen merke til?

Gode veiledningsspørsmål

  • Hvordan vet du at du ikke kan bruke flere tall for å lage 37?
  • Hvordan vet du at du ikke kan bruke færre tall for å lage 37?
  • Hva har tallene 1, 3, 5 og 7 til felles?

Mulig støtte

En lommeregner kan være nyttig for noen elever hvis du vil sette fokus på analysen snarere enn på utregningene.

Ressursen er utviklet av NRICH

8,9