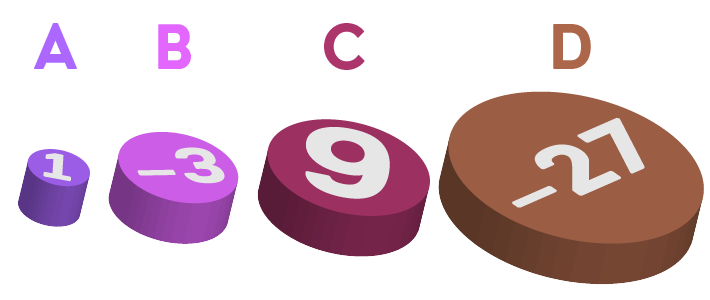Læreplankoblet

LAST NED kopioriginaler

Klosser

Stikkord: Negative tall Resonnering

Aktivitet

Se for deg at du har to av hver av klossene på figuren. Med ulike kombinasjoner av klossene kan du lage forskjellige tall.

Vekter med verdi 1, -3, 9 og -27.

Eksempel:

B + C = 6

B + 2C = 15

A + 2B + C = 4

2A + B + 2C + D = -10

Det største tallet du kan lage, er 20 (sjekk om du er enig).

Det minste tallet du kan lage, er -60 (sjekk om du er enig).

Kan du lage alle tallene mellom -60 og 20?

Er det alltid en unik måte å lage et bestemt tall på, eller kan ulike kombinasjoner gi samme tall.

Utvidelse

Du har bare lov til å bruke tre ulike klosser (E, F og G) og maks tre av hver. Minst én av dem må være et negativt tall. Da kan du velge dette:

E = 1

F = -4

G = 5

Du kan lage 7 og -10:

E + F + 2G = 7

2E + 3F = -10

Velg tre klosser, og finn ut hvilke tall du kan lage med dem.

Hvilket sett med tre klosser må du velge for å lage størst omfang/område/rekkevidde/verdiområde/variasjonsbredde uten hull imellom?
 

Starthjelp

Det største tallet du kan lage, er 20. 2A + 2C.

Det minste tallet du kan lage, er -60. 2B+2D.

Noen tall er enklere å lage enn andre (kanskje de som krever en kombinasjon av bare én eller to klosser), så det kan være en god idé å begynne med dem og så bygge videre på dem med noen ekstra klosser.
 

Lærerveiledning

Hvorfor arbeide med denne oppgaven?

Denne aktiviteten gir elevene mulighet til å addere positive og negative tall, samtidig som de må arbeide systematisk.

Mulig tilnærming

Arbeidsarket som du finner i lista over kopioriginaler kan være nyttig. 

Introduser situasjonen i aktiviteten. Negative klosser kan ses på som sterke heliumballonger som løfter opp klossene. 

Elevene kan foreslå noen eksempler som klassen kan arbeide med for å avklare hvordan prosedyrene fungerer. Hva er det største og det minste tallet? Gi elevene tid til å forklare hvorfor 20 og -60 er riktig.

Sett klassen i gang med å arbeide med hovedoppgaven:

Kan du lage alle tallene imellom? Kan du vise hvordan? Er det alltid en unik måte å lage et bestemt tall på, eller kan ulike kombinasjoner lage samme tall?

Det finnes forskjellige strategier for å håndtere denne oppgaven, så hvis du observerer ulike framgangsmåter, kan du la elevene forklare hvordan de tenker. Det kan lede til en diskusjon om mulige måter å gå fram på.

Gode veiledningsspørsmål

  • Kan du lage alle tallene imellom? Kan du vise hvordan?
  • Er det alltid en unik måte å lage et bestemt tall på, eller kan ulike kombinasjoner lage samme tall?

Mulig utvidelse

Utvidelsesoppgaven som er beskrevet ovenfor, passer godt her. Noen elever kan lære av å se på hvordan andre elever har tenkt, og hvordan de har forklart tenkingen sin.

Mulig støtte

Organiser elevene i små grupper med et stort ark de kan arbeide på. Gruppene skriver tallene fra 20 til -60, og fyller så inn summene de finner. Elevene må kontrollere summene til de andre i gruppen før de skriver summen på gruppearket.
 

Send inn elevsvar

Til enhver tid vil det være mulig å sende inn løsning på noen av oppgavene på Mattelist.

Elever står fritt til å sende inn egne løsninger, men vi vil også gjerne at lærere sender inn besvarelser fra klassen sin.

Løsningsforslag kan bli publisert på sidene. Det kan være stas for klassen, samtidig som at andre elever og lærere kan bli inspirert.


Her er en liten veiledning:

  • Vi ønsker en løsning, ikke kun et svar.
  • Skriv løsningen slik at andre kan forstå hvordan du har tenkt.
  • Send gjerne bilder av arbeidet ditt.
  • Bruk gjerne illustrasjoner, grafer, tabeller, tegninger eller andre ting som viser hvilke hjelpemidler du har brukt i løsningen.
Løsningsforslag kan bli publisert på sidene!

Ressursen er utviklet av NRICH

8