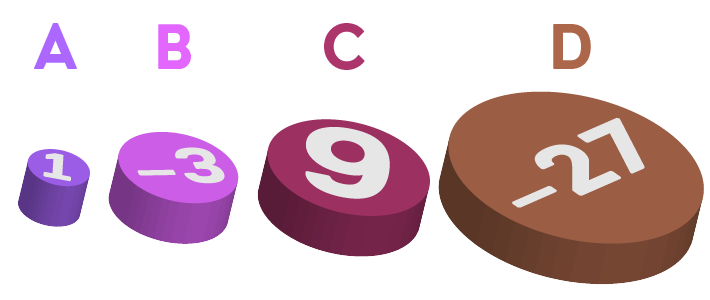Læreplankoblet

LAST NED kopioriginaler

Klossar

Stikkord: Negative tall Resonnering

Aktivitet

Sjå for deg at du har to av kvar av klossane på figuren. Med ulike kombinasjonar av klossane kan du lage forskjellige tal

Vekter med verdi 1, -3, 9 og -27.

Eksempel:

B + C = 6

B + 2C = 15

A + 2B + C = 4

2A + B + 2C + D = -10
 

Det største talet du kan lage, er 20 (sjekk om du er einig).

Det minste talet du kan lage, er -60 (sjekk om du er einig).

Kan du lage alle tala mellom -60 og 20?

Er det alltid ein unik måte å lage eit bestemt tal på, eller kan ulike kombinasjonar gi same talet?
 

Utviding

Du har berre har lov til å bruke tre ulike klossar (E, F og G) og maks tre av kvar. Minst éi av dei må vere eit negativt tal. Då kan du velje dette:

E = 1

F = -4

G = 5

Du kan lage 7 og -10:

E + F + 2G = 7

2E + 3F = -10

Vel tre klossar, og finn ut kva tal du kan lage med dei.

Kva for eit sett med tre klossar må du velje for å lage størst omfang/område/rekkjevidde/verdiområde/variasjonsbreidde utan hol imellom?
 

Starthjelp

Det største talet du kan lage, er 20. 2A + 2C.

Det minste talet du kan lage, er -60. 2B + 2D.

Nokre tal er enklare å lage enn andre (kanskje dei som krev berre ein kombinasjon av éi eller to klossar), så det kan vere ein god idé å begynne med dei og så byggje vidare på dei med nokre ekstra klossar.
 

Lærarrettleiing

Kvifor skal vi arbeide med denne oppgåva?

Denne aktiviteten gir elevane moglegheit til å addere positive og negative tal, samtidig som dei må arbeide systematisk.
 

Mogleg tilnærming

Arbeidsarket som du finn i lista over kopioriginalar kan vere nyttig.

Introduser situasjonen i aktiviteten. Negative klossar kan de sjå som sterke heliumballongar som løfter opp klossane.

Elevane kan foreslå nokre eksempel som klassen kan arbeide med for å avklare korleis prosedyrane fungerer. Kva er det største og det minste talet? Gi elevane tid til å forklare kvifor 20 og -60 er rett.

Set klassen i gang med å arbeide med hovudoppgåva:

Kan du lage alle tala imellom? Kan du vise korleis? Er det alltid ein unik måte å lage eit bestemt tal på, eller kan ulike kombinasjonar lage same talet?

Det finst forskjellige strategiar for å handtere denne oppgåva, så dersom du observerer ulike framgangsmåtar, kan du la elevane forklare korleis dei tenkjer. Dette kan leie til ein diskusjon om moglege måtar å gå fram på.
 

Gode rettleiingsspørsmål

  • Kan du lage alle tala imellom? Kan du vise korleis?
  • Er det alltid ein unik måte å lage eit bestemt tal på, eller kan ulike kombinasjonar lage same tal?
     

Mogleg utviding

Utvidingsoppgåva som er omtalt ovanfor, passar godt her. Somme elevar kan lære av å sjå på korleis andre elevar har tenkt, og korleis dei har forklart tenkinga si.

Mogleg støtte

Organiser elevane i små grupper med eit stort ark dei kan arbeide på. Gruppene skriv tala frå 20 til -60, og fyller så inn summane dei finn. Elevane må kontrollere summane til dei andre i gruppa før dei skriv summen på gruppearket.

 

Send inn elevsvar

Til enhver tid vil det være mulig å sende inn løsning på noen av oppgavene på Mattelist.

Elever står fritt til å sende inn egne løsninger, men vi vil også gjerne at lærere sender inn besvarelser fra klassen sin.

Løsningsforslag kan bli publisert på sidene. Det kan være stas for klassen, samtidig som at andre elever og lærere kan bli inspirert.


Her er en liten veiledning:

  • Vi ønsker en løsning, ikke kun et svar.
  • Skriv løsningen slik at andre kan forstå hvordan du har tenkt.
  • Send gjerne bilder av arbeidet ditt.
  • Bruk gjerne illustrasjoner, grafer, tabeller, tegninger eller andre ting som viser hvilke hjelpemidler du har brukt i løsningen.
Løsningsforslag kan bli publisert på sidene!

Ressursen er utviklet av NRICH

8