Utforsk kubiske funksjoner
Aktivitet
I GeoGebra-appleten nedenfor kan du flytte på glideren for å endre funksjonen.
Hva forblir likt? Hva endrer seg?
Hvilken funksjon tegnes hver gang? Du kan kontrollere det ved å trykke på «Vis funksjonsuttrykk».
Nedenfor er det en annen funksjon du kan utforske. I dette tilfellet blir summen av de tre skjæringspunktene 0.
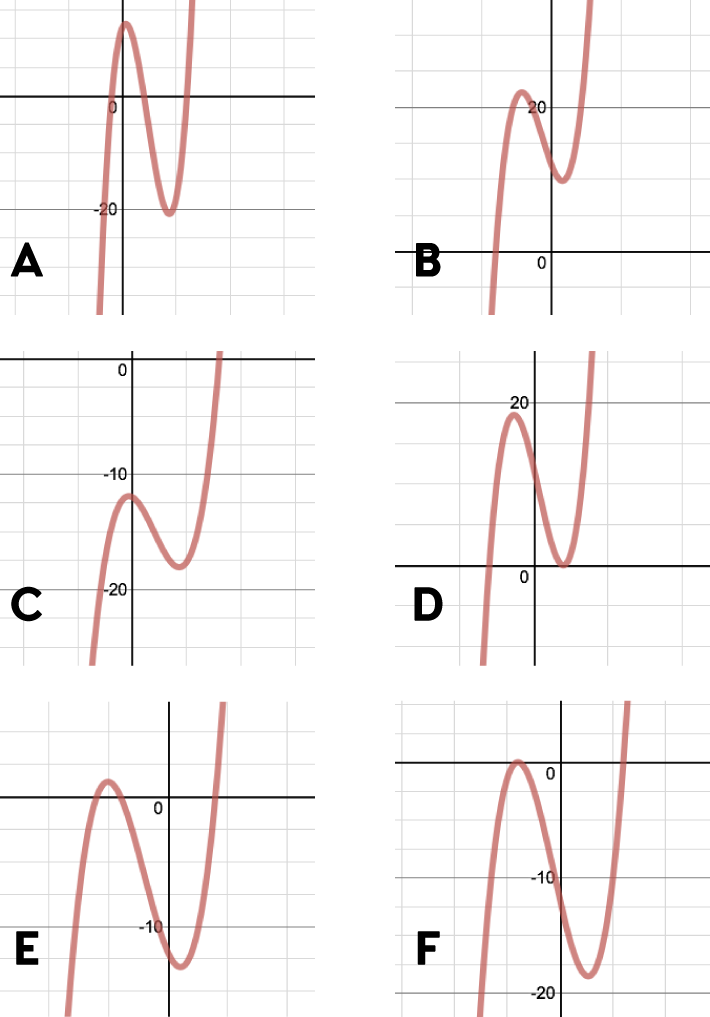
Her ser du seks grafer og funksjonsuttrykkene deres. Kan du sette sammen riktig graf og funksjonsuttrykk?
\(\begin{equation} 1)\:y=x^3+2x^2-5x+12\\ 2)\:y=x^3+3x^2-4x-12\\ 3)\:y=x^3-7x^2+4x+12\\ 4)\:y=x^3-3x^2-x-12\\ 5)\:y=x^3+x^2-8x-12\\ 6)\:y=x^3-x^2-8x+12 \end{equation}\)
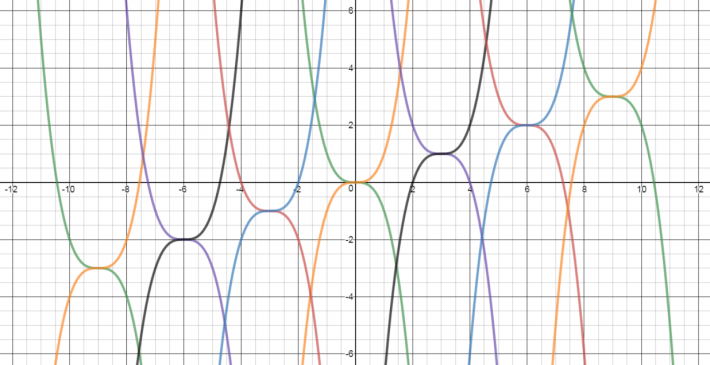
Her er en illustrasjon av grafene til 14 funksjoner. To av dem har disse likningene:
\(y=(x+6)^3-2\\ y=-(x-9)^3+3 \)
Kan du finne likningene til de 12 andre grafene i dette mønsteret?
Forsøk å lage lignende mønster selv, der du bruker ulike grupper av kubiske funksjoner (tredjegradsfunksjoner).
Starthjelp
Noe å tenke på når du arbeider med funksjoner:
- Hvor skjærer grafen x-aksen?
- Hvor skjærer grafen y-aksen?
- Har grafen speilingssymmetri eller rotasjonssymmetri?
- Har grafen noen ekstremalpunkter?
I arbeid med funksjoner i GeoGebra kan det være lurt å begynne med glideren på 0.
Når du har to glidere i GeoGebra, bør du utforske effekten av hver enkelt før du utforsker effekten av å endre begge samtidig.
Lærerveiledning
Hvorfor arbeide med denne oppgaven?
Mange elever arbeider mye med kvadratiske funksjoner, men kanskje ikke like mye ned kubiske funksjoner. Denne oppgaven presenterer noen eksempler på tredjegradsfunksjoner, og elevene kan utforske grafene deres.
Ved å veksle mellom forskjellige algebraiske og grafiske representasjoner kan elevene få innsikt i sammenhenger som ikke nødvendigvis er så åpenbare hvis de arbeider bare algebraisk. Sammen med støtten som tilbys gjennom interaktive GeoGebra-appleter, legger oppgaven til rette for arbeid som gjør elevene mer fleksible når de skal tolke og tegne funksjoner – et emne som mange synes er utfordrende.
Mulig tilnærming
Elevene vil få mest mulig utbytte av denne oppgaven dersom de har tilgang til datamaskiner eller nettbrett, enten individuelt eller gruppevis, slik at de kan utforske GeoGebra-appletene. Alternativt kan oppgaven vises på storskjerm, og funksjonene kan utforskes som en felles aktivitet. Læreren må da endre på gliderne, og elevene må oppfordres til å legge merke til forandringer og gjette hva som vil skje.
Be elevene flytte på glideren på den første appleten for å endre funksjonen, og skrive ned det de legger merke til. Bruk spørsmålene i teksten:
- Hva forblir likt?
- Hva endrer seg?
- Hva kan funksjonsuttrykket være?
Styr fokuset mot grafens skjæringspunkter med x-aksen og sammenhengen mellom funksjonen \(f(x)=x(x-a)(x+a) \) og formen på grafen. Så skal elevene utvide funksjonsuttrykket.
Prosessen blir den samme med den andre appleten. Mens elevene flytter på glideren, skal de legge merke til hva som forblir likt, og hva som endrer seg, og se etter sammenhenger mellom nøkkelpunkter, som skjæringspunkt og ekstremalpunkt, og funksjonsuttrykket.
La elevene få god tid til å utforske appletene og se på sammenhengen mellom funksjonsuttrykkene og grafene deres. Del ut kopioriginal 1, og utfordre elevene til å sette sammen riktig graf og funksjonsuttrykk. Du kan avslutte timen med at elevene eller gruppene argumenterer for løsningene sine.
Den siste aktiviteten i oppgaven finner du som kopioriginal 2. Den kan du bruke i en annen time, for eksempel som lekse.
Gode veiledningsspørsmål
- Hvor skjærer grafen x-aksen?
- Hvor skjærer grafen y-aksen?
- Har grafen speilingssymmetri eller rotasjonssymmetri?
- Har grafen noen ekstremalpunkter?
Mulig støtte
Elevene kan begynne med å utforske kvadratiske funksjoner før de går over til kubiske. Parabolmønstre er en fin utfordring som legger til rette for lignende tenking.
Ressursen er utviklet av NRICH