Utforske kubiske funksjonar
Aktivitet
I GeoGebra-appleten nedanfor kan du flytte på glidaren for å endre funksjonen.
Kva blir framleis likt? Kva endrar seg?
Finn ut kva for ein funksjon som blir teikna kvar gong. Du kan kontrollere det ved å trykkje på «Vis funksjonsuttrykk».
Nedanfor er det ein annan funksjon du kan utforske. I dette tilfellet blir summen av dei tre skjeringspunkta 0.
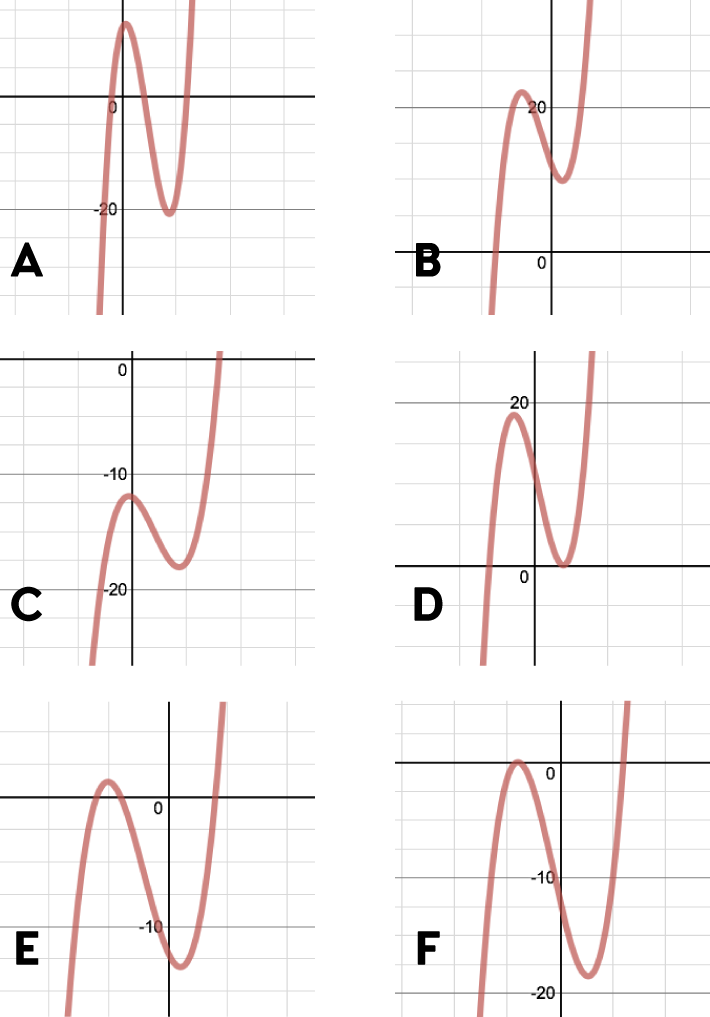
Her ser du seks grafar og funksjonsuttrykka deira. Kan du setje saman rett graf og funksjonsuttrykk?
\(\begin{equation} 1)\:y=x^3+2x^2-5x+12\\ 2)\:y=x^3+3x^2-4x-12\\ 3)\:y=x^3-7x^2+4x+12\\ 4)\:y=x^3-3x^2-x-12\\ 5)\:y=x^3+x^2-8x-12\\ 6)\:y=x^3-x^2-8x+12 \end{equation}\)
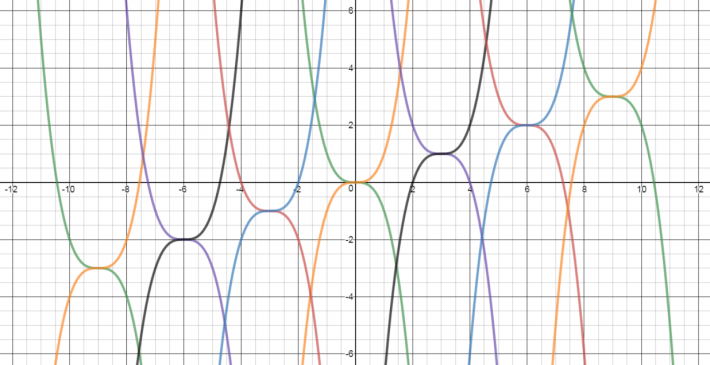
Her er ein illustrasjon av grafane til 14 funksjonar. To av dei har desse likningane:
\(y=(x+6)^3-2\\ y=-(x-9)^3+3 \)
Kan du finne likningane til dei 12 andre grafane i dette mønsteret?
Prøv å lage liknande mønster sjølv, der du brukar ulike grupper av kubiske funksjonar (tredjegradsfunksjonar)?
Starthjelp
Noko å tenkje på når du arbeider med funksjonar:
- Kvar skjer grafen x-aksen?
- Kvar skjer grafen y-aksen?
- Har grafen speglingssymmetri eller rotasjonssymmetri?
- Har grafen nokre ekstremalpunkt?
I arbeid med funksjonar i GeoGebra kan det vere lurt å begynne med glidaren på 0.
Når du har to glidarar i GeoGebra, bør du utforske effekten av kvar av dei før du utforskar effekten av å endre begge samtidig.
Lærarrettleiing
Kvifor arbeide med denne oppgåva?
Mange elevar arbeider mykje med kvadratiske funksjonar, men kanskje ikkje like mykje med kubiske funksjonar. Denne oppgåva presenterer nokre eksempel på tredjegradsfunksjonar, og elevane kan utforske grafane deira.
Ved å veksle mellom forskjellige algebraiske og grafiske representasjonar kan elevane få innsikt i samanhengar som ikkje nødvendigvis er så openberre dersom dei arbeider berre algebraisk. Saman med støtta dei kan få gjennom interaktive GeoGebra-appletar, legg oppgåva til rette for arbeid som gjer elevane meir fleksible når dei skal tolke og teikne funksjonar – eit emne som mange synest er utfordrande.
Mogleg tilnærming
Elevane vil få mest mogleg utbyte av denne oppgåva dersom dei har tilgang til datamaskinar eller nettbrett, anten individuelt eller gruppevis, slik at dei kan utforske GeoGebra-appletane. Alternativt kan oppgåva visast på ein storskjerm, og funksjonane kan utforskast som ein felles aktivitet. Læraren må då endre på glidarane, og elevane må oppfordrast til å leggje merke til forandringar og gjette kva som vil skje.
Be elevane flytte på glidaren på den første appleten for å endre funksjonen, og skrive ned det dei legg merke til. Bruk spørsmåla i teksten:
- Kva blir verande likt?
- Kva endrar seg?
- Kva kan funksjonsuttrykket vere?
Styr fokuset mot skjeringspunkt mellom grafen og x-aksen, og samanhengen mellom funksjonen \(f(x)=x(x-a)(x+a) \) og forma på grafen. Så skal elevane utvide funksjonsuttrykket. Prosessen blir den same med den andre appleten. Medan elevane flytter på glidarane, skal dei leggje merke til kva som blir verande likt, og kva endrar seg, og sjå etter samanhengar mellom nøkkelpunkt, som skjeringspunkt og ekstremalpunkt, og funksjonsuttrykket.
La elevane få god tid til å utforske appletane og sjå på samanhengen mellom funksjonsuttrykka og grafane deira. Del ut kopioriginal 1, og utfordre elevane til å setje saman rett graf og funksjonsuttrykk. Du kan avslutte timen med at elevane eller gruppene argumenterer for løysingane sine.
Den siste aktiviteten i oppgåva finn du som kopioriginal 2. Den kan du bruke i ein annan time eller for eksempel som lekse.
Gode rettleiingsspørsmål
- Kvar skjer grafen x-aksen?
- Kvar skjer grafen y-aksen?
- Har grafen speglingssymmetri eller rotasjonssymmetri?
- Har grafen nokre ekstremalpunkt?
Mogleg støtte
Elevane kan begynne med å utforske kvadratiske funksjonar før dei går over til kubiske funksjonar. Parabolmønster er ei fin utfordring, som legg til rette for liknande tenking.
Ressursen er utviklet av NRICH