Hunden spiste leksene mine!
Aktivitet
Læreren Løgnde Tektor sier at han enkelt kan avsløre når elever lyver om leksene sine, og det kan han!
Dessverre så anklager han også noen elever som forteller sannheten.
Så, hva er sannsynligheten for at han anklager noen som forteller sannheten?
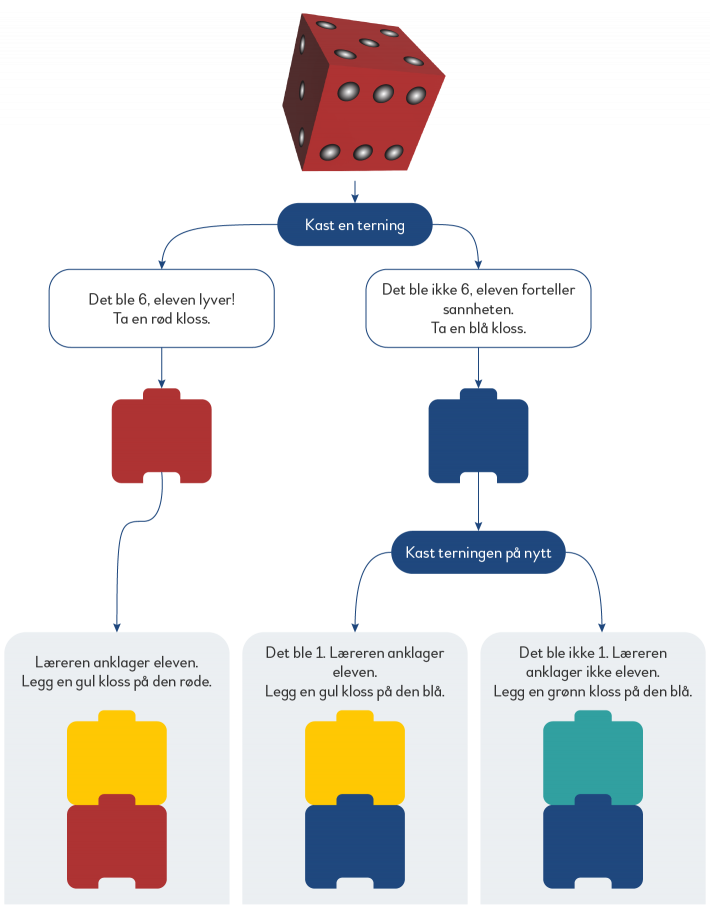
Du kan undersøke dette spørsmålet gjennom et praktisk eksperiment. Du trenger en vanlig terning og noen røde, blå, grønne og gule klosser (f.eks. multilink). De røde og blå klossene representerer om en elev forteller sannheten eller lyver. De gule og grønne klossene representerer om læreren anklager eleven eller ikke.
Undersøk først hva som kan skje med én tilfeldig elev:
Hva betyr
- Rød og gul?
- Blå og gul?
- Blå og grønn?
Hvorfor kan du ikke få rød og grønn?
- Gjør noen beregninger og skriv ned hvordan vi kan forvente at resultatet blir for en klasse med 36 elever. Du kan bruke kopioriginal 1 til dette.
- Gjør eksperimentet 36 ganger, slik at du ender opp med 36 par klosser. Registrer resultatet på samme måte som du gjorde på punktet over.
- Ble du overrasket over resultatet?
- Hvor stor del av de ærlige elevene ble anklaget? Hva kan du dermed si om sannsynligheten for at en ærlig elev blir anklaget?
- Hvor stor andel av de anklagede elevene forteller sannheten?
- Er sannsynligheten for at en ærlig elev blir anklaget lik sannsynligheten for at en anklaget elev forteller sannheten? Blir du overrasket av det du finner ut?
- Når du når har gjort eksperimentet med terning 36 ganger, kan du lage et dataprogram som lar deg gjøre det samme enda flere ganger? 1000, 10 000, 100 000 ganger? Får du et annet resultat da?
Lærerveiledning
Hvorfor arbeide med denne oppgaven
Denne aktiviteten modellerer tolkningen av statistikk for f.eks. kreft, HIV, graviditet, DNA og mange andre lignende situasjoner som involverer falske positive. I stedet for å fokusere på disse temaene som kan være litt vanskelige, arbeider vi i denne oppgaven med et tulletema slik at elevene kan fokusere på matematikken, og deretter diskutere hva resultatene betyr og hvilke applikasjoner matematikken kan ha i den virkelige verden. Gjennom å lage et dataprogram som gjennomfører eksperimentet, får elevene utfordringer med å kombinere løkker og betingelser.
Mulig tilnærming
Del elevene inn i grupper 3 til 4. Hver gruppe trenger en vanlig terning og noen røde, blå, grønne og gule klosser. La elevene få diskutere, eventuelt beregne og notere forventningene sine før de begynner å samle inn data med terningkast og klosser. Det kan også være lurt å gå gjennom eksperimentet med én «elev» i plenum, før gruppene begynner å samle inn data.
Elevene kan notere funnene sine i kopioriginalen når de har gjennomført eksperimentet 36 ganger.
For å generere data fra et større antall eksperimenter, kan elevene forsøke seg på å lage et dataprogram som gjennomfører x antall eksperimenter og lagrer resultatene. Dette kan f.eks. gjøres ved hjelp av Scratch, Python eller regneark. Hvor mange forsøk må vi gjennomføre for å nærme oss den teoretiske sannsynligheten?
Gode veiledningsspørsmål
- Hvordan stemmer resultatene fra eksperimentet med forventningene?
- Hvor mange elever ble anklaget til sammen? Er det overraskende? Hvorfor/hvorfor ikke?
- Hvor mange ærlige elever blir anklaget? Hvor stor del av ærlige elever blir anklaget? Hva er sannsynligheten for at en ærlig elev blir anklaget?
- Hvor mange anklagede elever forteller sannheten? Hvor stor andel av anklagede elever forteller sannheten?
- Er sannsynligheten for at en ærlig elev blir anklaget lik sannsynligheten for at en anklaget elev forteller sannheten? Er det overraskende? Hvorfor/hvorfor ikke?
- Hvilke tall er like i diagrammet og tabellen, og hvilke er ulike?
- Hva er fordelene med diagrammet? Hva er fordelene med tabellen? Hvilken informasjon kan du enkelt finne i de to forskjellige representasjonene, og hva er vanskeligere eller umulig å finne?
Mulig utvidelse
- Hvilken forskjell ville det utgjøre dersom Løgnde Tektor ikke alltid greide å avsløre elever som lyver? Hvordan kan du endre modellen?
- Kritiser modellen. Hvilke antakelser gjør den? Kan du forbedre den slik at den blir mer realistisk?
- Skjer det usannsynlige og Rødt utslett eller meslinger er oppgaver som innebærer betinget sannsynlighet i kontekst, som kan være passende utvidelser.
Mulig støtte
Alle elevene kan utføre eksperimentet, når de først har forstått scenarioet og hatt en felles gjennomføring med et eksempel. Kopioriginalen er laget for å hjelpe elevene med å tolke resultatene sine. Elever som synes spørsmålene i oppgaven/veiledningsspørsmålene er vanskelige kan heller fokusere på sammenlikningen mellom eksperimentell og forventet resultat og å kritisere modellen. Er det for eksempel rimelig å forvente at en sjettedel av alle elevene lyver om leksene sine? Om det ikke er det, hvordan kan vi endre på eksperimentet?
Ressursen er utviklet av NRICH