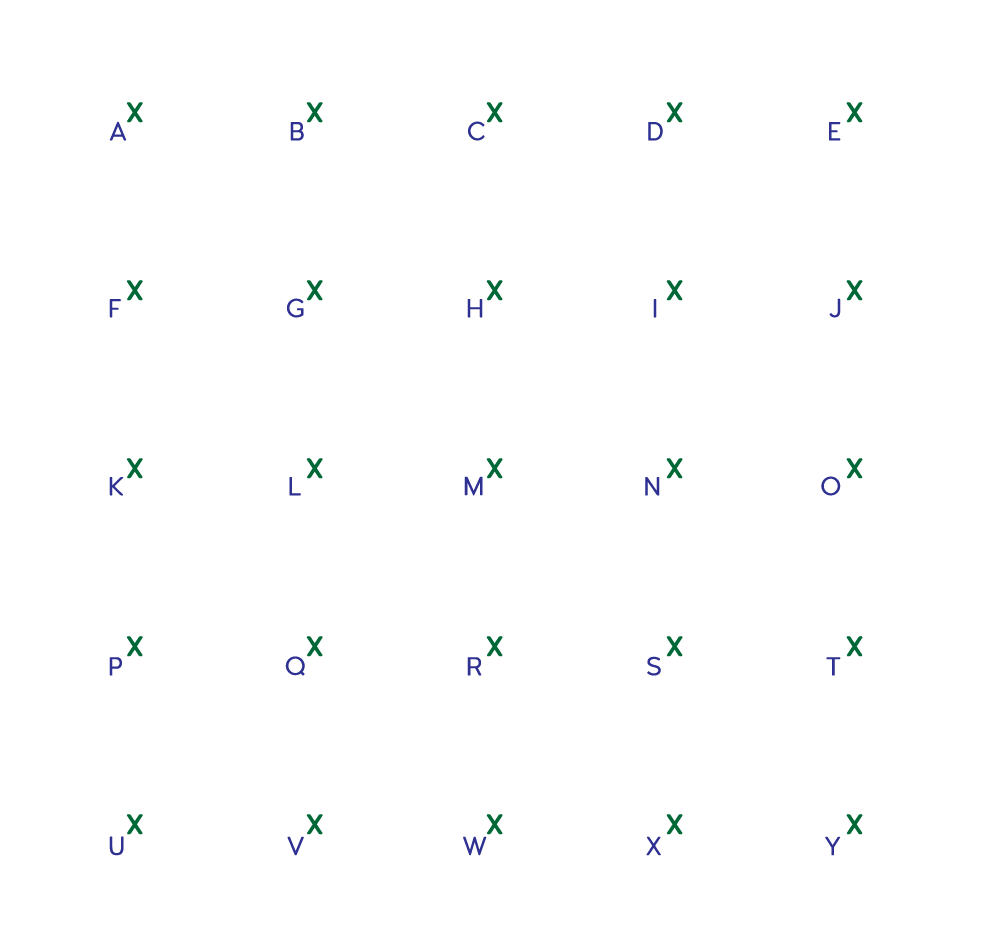Hvor bratt er stigningen?
Aktivitet
Stigningstallet til en linje forteller oss hvor langt opp eller ned vi går når vi tar ett skritt til høyre:
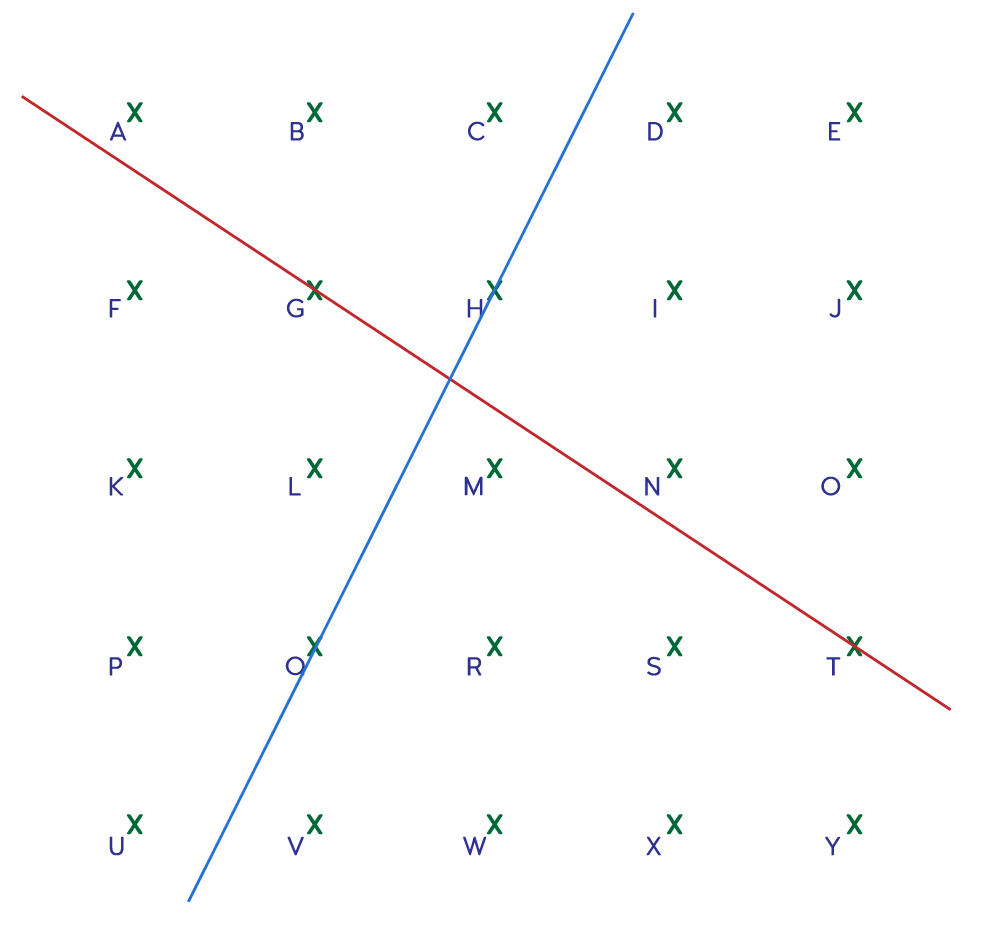
På et rutenett som det nedenfor kan vi tegne linjer gjennom to punkter slik at linjene får forskjellige stigningstall. Finn ut om du er enig i at den blå linja er en av flere linjer som kan tegnes med stigningstall 2, og at den røde linja er en av flere linjer som kan tegnes med stigningstall −23
Se for deg noen flere linjer med forskjellige stigningstall. Du kan notere arbeidet ditt på kopioriginal 1.
Hvor mange forskjellige stigningstall kan du finne? Kan du finne alle som er mulige i rutenettet?
Sorter dem etter hvor bratte de er, og lag en oversikt over hvilke punkter hver linje går gjennom.
Starthjelp
Legg linjalen din over U. Hvilket punkt bør du forbinde U med for å få den brattest mulige stigningen? For å få den nest bratteste? Den neste?
Hvor kan du plassere den ene enden av linjalen din for å finne alle mulige negative stigningstall?
Lærerveiledning
Hvorfor arbeide med denne oppgaven?
Denne oppgaven introduserer stigningstall i enkle omgivelser, der elevene kan utforske de viktigste aspektene ved stigningstall.
Mulig tilnærming
Det kan være nyttig å dele ut kopioriginalene.
Introduser elevene for definisjonen av stigningstall. Motstå fristelsen til å gi dem en «regel» for å finne et stigningstall, siden metoder for å finne det bør komme etter diskusjonene nedenfor.
Vis fram bildet av rutenettet under. Klikk på bildet for å åpne det i en ny fane, eller skriv ut kopioriginalen.
Noen av disse spørsmålene kan brukes for å få elevene til å tenke på forskjellige stigningstall:
- Jeg ser for meg en linje med stigningstall 2 som går gjennom H. Hvilket annet punkt går linja gjennom?
- Hvor mange andre linjer med stigningstall 2 kan du finne?
- Kan du finne en eller flere linjer som er brattere eller mindre bratte?
- Kan du finne noen linjer med stigningstall mellom 1 og 2?
- Hva er stigningstallet til linja som går gjennom G og O?
- Kan du finne en eller flere brattere eller mindre bratte (negative) linjer?
- Hvorfor kan det være problematisk å finne stigningstallet til linja som går gjennom R og M?
Bruk disse spørsmålene som et utgangspunkt for å diskutere forskjellige strategier for å finne stigningstall.
Del ut kopier av rutenettet (kopioriginal 1), og la elevene arbeide i par med hovedproblemet: «Hvor mange forskjellige stigningstall kan dere finne? Finn alle som er mulige i rutenettet. Sorter dem etter hvor bratte de er, og lag en oversikt over hvilke punkter hver linje går gjennom.»
Oppfordre elevene til å arbeide systematisk, slik at de får gode forutsetninger for å argumentere for funnene sine. Gå rundt i klasserommet når elevene diskuterer, og merk deg interessante tilnærminger som de får dele med resten av klassen på slutten av arbeidsøkta.
Gode veiledningsspørsmål
- Hvilken betydning har det for en linje om stigningstallet er positivt eller negativt?
- Hva kan vi si om linjer med positive stigningstall som er større eller mindre enn 1 (eller negative stigningstall som er større eller mindre enn –1)?
- En standardmåte å finne stigningstall på er å dividere den vertikale forskyvningen med den horisontale forskyvningen. Hva er sammenhengen mellom denne algoritmen og definisjonen av stigningstall ovenfor?
Mulig utvidelse
Elevene kan arbeide videre med oppgaven «Parallelle linjer», der de skal undersøke forholdet mellom likningene til parallelle og vinkelrette linjer i et koordinatsystem.
Mulig støtte
Elever som strever med å arbeide systematisk, kan legge den ene enden av linjalen på et ytterpunkt i rutenettet, og flytte den andre enden langsomt for å lage linjer med forskjellige stigningstall.
Ressursen er utviklet av NRICH