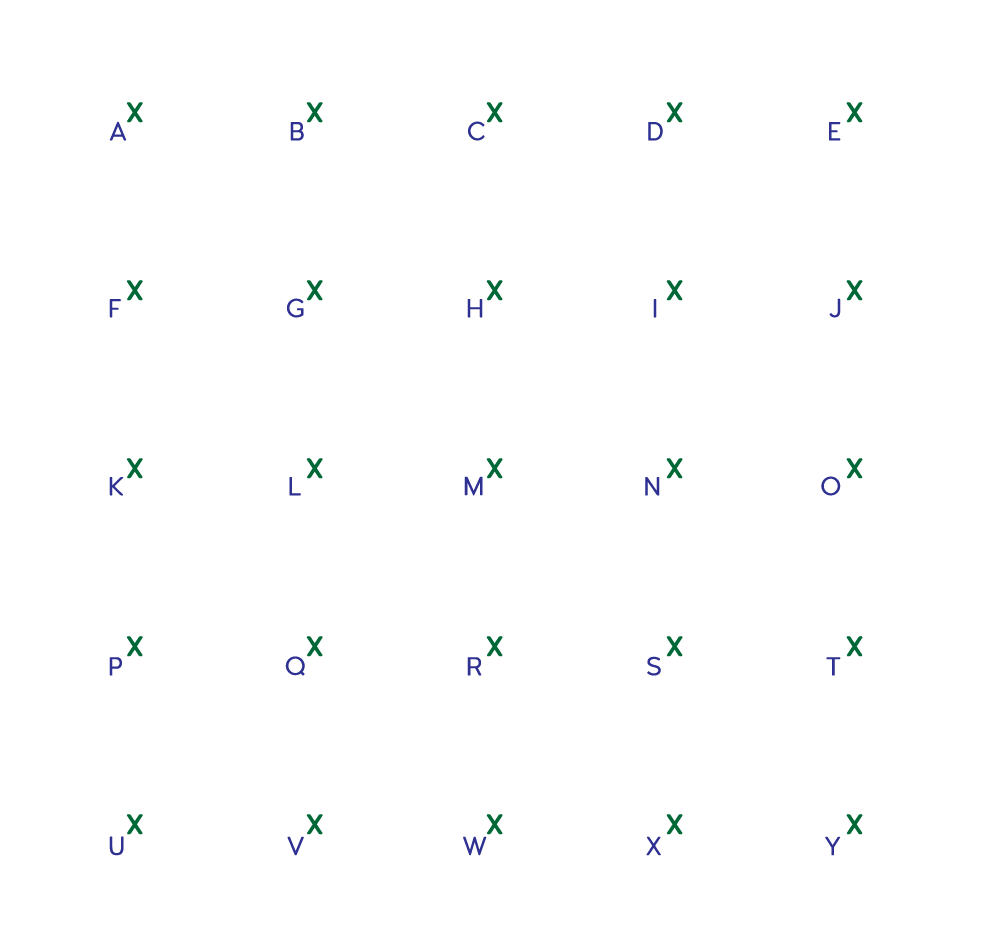Kor bratt er stigninga?
Aktivitet
Stigningstalet til ei linje fortel oss kor langt opp eller ned vi går når vi tek eitt steg til høgre:
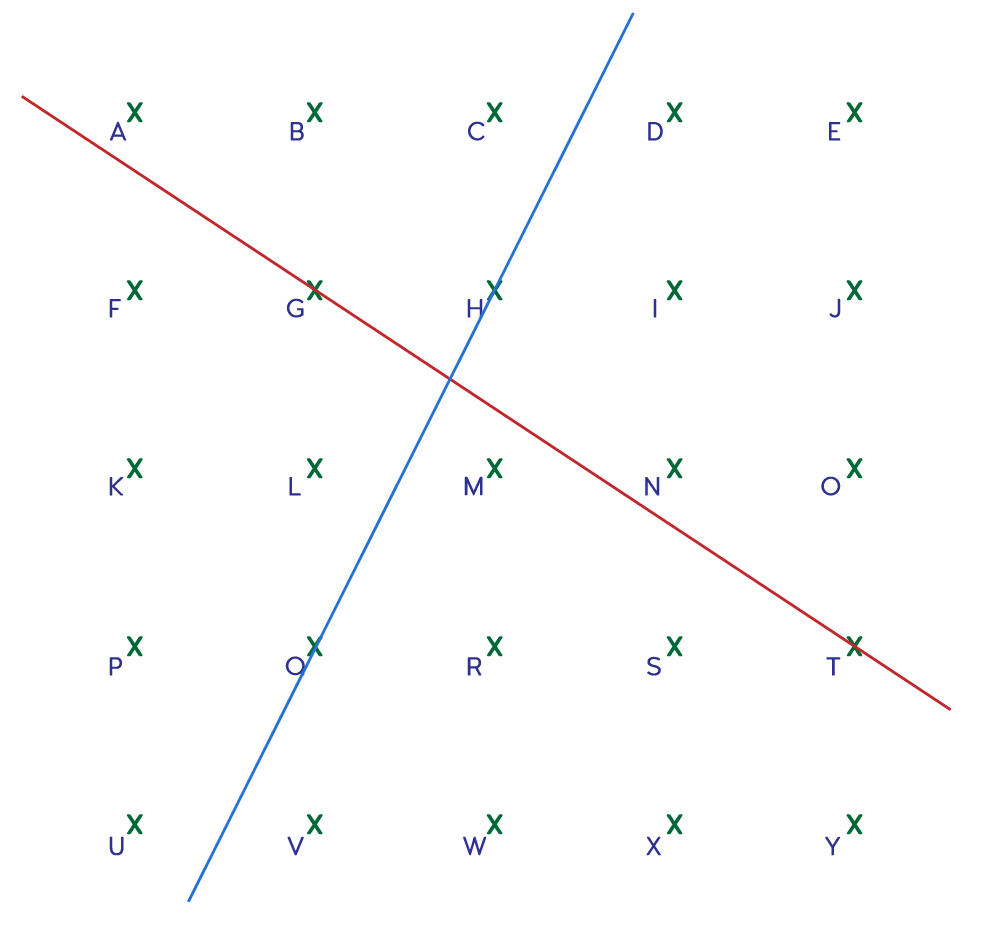
På eit rutenett som det nedanfor kan vi teikne linjer gjennom to punkt slik at linjene får forskjellige stigningstal. Finn ut om du er einig i at den blå linja er ei av fleire linjer som kan teiknast med stigningstal 2, og at den raude linja er ei av fleire linjer som kan teiknast med stigningstal \(-\frac23\)
Sjå for deg nokre fleire linjer med forskjellige stigningstal. Du kan notere arbeidet ditt på kopioriginal 1.
Kor mange forskjellige stigningstal kan du finne? Kan du finne alle som er moglege i rutenettet?
Sorter dei etter kor bratte dei er, og lag ei oversikt over dei punkta som kvar linje går gjennom.
Starthjelp
Legg linjalen din over U. Kva for eit punkt bør du forbinde U med for å få den brattast moglege stigninga? For å få den nest brattaste? Den neste?
Kvar kan du plassere den eine enden av linjalen din for å finne alle moglege negative stigningstal?
Lærarrettleiing
Kvifor arbeide med denne oppgåva?
Denne oppgåva introduserer stigningstal i enkle omgivnader, der elevane kan utforske dei viktigaste aspekta ved stigningstal.
Mogleg tilnærming
Det kan vere nyttig å dele ut kopioriginalane.
Introduser elevane for definisjonen av stigningstal. Ikkje la deg freiste til å gi dei ein «regel» for å finne eit stigningstal, sidan metodar for å finne det bør kome etter diskusjonane nedanfor.
Vis fram biletet av rutenettet under. Klikk på biletet for å opne det i ei ny fane, eller skriv ut kopioriginalen.
Nokre av desse spørsmåla kan brukast for å få elevane til å tenkje på forskjellige stigningstal:
- Eg ser for meg ei linje med stigningstal 2 som går gjennom H. Kva for eit anna punkt går linja gjennom?
- Kor mange andre linjer med stigningstal 2 kan du finne?
- Kan du finne ei eller fleire linjer som er brattare eller mindre bratte?
- Kan du finne nokre linjer med stigningstal mellom 1 og 2?
- Kva er stigningstalet til linja som går gjennom G og O?
- Kan du finne ei eller fleire brattare eller mindre bratte (negative) linjer?
- Kvifor kan det vere problematisk å finne stigningstalet til linja som går gjennom R og M?
Bruk desse spørsmåla som eit utgangspunkt for å diskutere forskjellige strategiar for å finne stigningstal.
Del ut kopiar av rutenettet (kopioriginal 1), og la elevane arbeide i par med hovudproblemet: «Kor mange forskjellige stigningstal kan de finne? Finn alle som er moglege i rutenettet. Sorter dei etter kor bratte dei er, og lag ei oversikt over punkta som kvar linje går gjennom.»
Oppfordre elevane til å arbeide systematisk, slik at dei får gode føresetnader for å argumentere for funna sine. Gå rundt i klasserommet når elevane diskuterer, og merk deg interessante tilnærmingar som dei får dele med resten av klassen på slutten av arbeidsøkta.
Gode rettleiingsspørsmål
- Kva har det å seie for ei linje om stigningstalet er positivt eller negativt?
- Kva kan vi seie om linjer med positive stigningstal som er større eller mindre enn 1 (eller negative stigningstal som er større eller mindre enn –1)?
- Ein standardmåte å finne stigningstal på er å dividere den vertikale forskyvinga med den horisontale forskyvinga. Kva er samanhengen mellom denne algoritmen og definisjonen av stigningstal ovanfor?
Mogleg utviding
Elevane kan arbeide vidare med oppgåva «Parallelle linjer», der dei skal undersøkje forholdet mellom likningane til parallelle og vinkelrette linjer i eit koordinatsystem.
Mogleg støtte
Elevar som strevar med å arbeide systematisk, kan leggje den eine enden av linjalen på eit ytterpunkt i rutenettet, og flytte den andre enden litt etter litt for å lage linjer med forskjellige stigningstal.
Ressursen er utviklet av NRICH