Rik eller raka fant

Hvorfor skal vi arbeide med denne oppgaven?

I denne oppgaven skal elevene utforske begrepet prosentvis endring, og spesielt det å ta i bruk sammenhengen mellom multiplikasjon og prosentvis endring. De skal finne ut om lik prosentvis endring alltid er det samme (f.eks. hvis 10 % reduksjon ikke er det motsatte av 10 % økning, hva er da det motsatte?).

Mulig tilnærming

Begynn med noen gjentakende 10 %-økninger eller -reduksjoner. Eksempler: «En bil mister 10 % av verdien sin hvert år. Hvis prisen på bilen var 100 000, hvor mye er den verdt etter tre år?» «Den årlige renten på et fond er på 10 %. Hvor mange prosent har sparepengene økt på fire år?»

Diskuter metodene som elevene har brukt for å finne svar på disse spørsmålene. Forhåpentligvis vil multiplikasjonsmetoden komme fram, der 10 % økning kan representeres som 110 % av den opprinnelige mengden. Vi kan altså multiplisere med \(\frac{110}{100}=\frac{11}{10}\) eller med 1,1.

Spør elevene hvor lang tid det vil ta før et investert beløp med en rente på 10 % har blitt doblet i verdi. De kan forsøke med prøving og feiling eller bruke en tabell for å komme fram til at svaret må være 8 år.

Deretter kan du stille det andre spørsmålet, hvor lang tid det vil ta før et beløp er halvert hvis det synker 10 % i verdi hvert år. Svaret på det skal være 7 år.

Disse svarene kan være et utgangspunkt for diskusjon. Er elevene overrasket over at svarene er ulike? Hvorfor får de ikke samme svar? Hvis vi endrer 10 % til et annet tall, vil svarene bli like da? Kan svarene noen gang bli like?

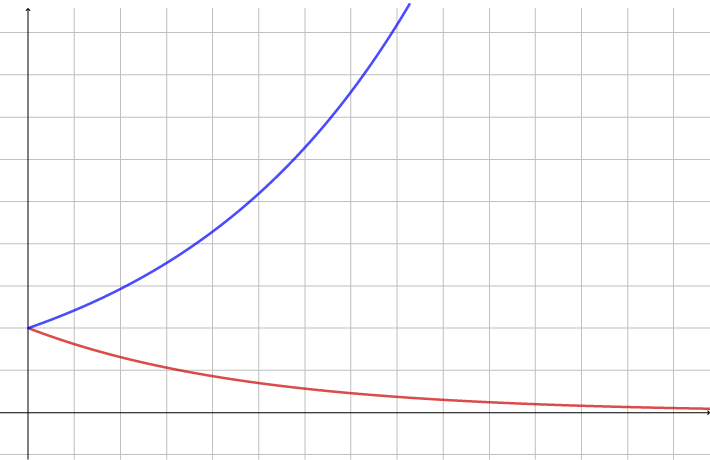
La elevene utforske, gjerne ved å prøve med flere forskjellige prosenter. Det kan være nyttig å bruke regneark og/eller et grafisk tegneprogram (f.eks. GeoGebra). Du kan oppfordre elevene til å representere problemet algebraisk. Grafisk bør de se at grafene ikke er like. Et viktig algebraisk poeng er at uttrykkene ikke er omvendte eller motparter (\(\frac12\) og 2 er motparter, men \(1,1^x\) og \(0,9^x\) er ikke det), og det fører til et bevis for at svarene aldri blir like.

Be elevene om å dele arbeidet sitt, og trekk fram og dra linjer mellom de ulike representasjonene de har brukt. Kan de forklare hvorfor de to svarene er ulike? Har noen funnet et tall (en prosent) slik at tiden som trengs for dobling og halvering, blir lik? Eller har noen klart å bevise at dette er umulig?

Gode veiledningsspørsmål

• Er en økning på 10 % det motsatte av en reduksjon på 10 %? Hva vil skje om du tar et tall, øker det med 10 % og reduserer det med 10 % etterpå?
• Er multiplisering med 1,1 det motsatte av multiplisering med 0,9? Hvorfor?

Mulig støtte

Hvis noen elever ikke kjenner multiplikasjonsmetoden for å regne ut prosentvis økning og reduksjon, kan det være en god idé å la dem bli kjent med den først.

For noen kan det være vanskelig å beregne prosentvis endring når det ikke er oppgitt en startverdi. Om dette er tilfellet, kan de kan velge en startverdi og bruke den. Så kan de endre startverdien og se om de får det samme resultatet. Deretter kan de bruke en valgfri bokstav som startverdi (kan være et hvilket som helst tall) og se om de fortsatt får det samme resultatet. I resten av arbeidet kan du la elevene bruke en bokstav som startverdi, eller et valgfritt tall (du kan for eksempel anbefale å bruke 1 eller 100).