Rik eller raka fant

Kvifor arbeide med denne oppgåva?

I denne oppgåva skal elevane utforske omgrepet prosentvis endring, og særleg det å ta i bruk samanhengen mellom multiplikasjon og prosentvis endring. Dei skal finne ut om lik prosentvis endring alltid er det same (f.eks. dersom 10 % reduksjon ikkje er det motsette av 10 % auke, kva er då det motsette?).

Mogleg tilnærming

Begynne med nokre gjentakande 10 %-aukingar eller -reduksjonar. Eksempel: «En bil mistar 10 % av verdien sin kvart år. Dersom prisen på bilen var 100 000, kor mykje er han verd etter tre år?» «Den årlege renta på eit fond er 10 %. Kor mange prosent har sparepengane auka på fire år?»

Diskuter metodane som elevane har brukt for å finne svar på desse spørsmåla. Vonleg vil multiplikasjonsmetoden kome fram, der 10 % auke kan representerast som 110 % av den opphavlege mengda. Vi kan altså multiplisere med \(\frac{110}{100}=\frac{11}{10}\) eller med 1,1.

Spør elevane kor lang tid det vil ta før eit investert beløp med ei rente på 10 % har blitt dobla i verdi. Dei kan velje prøving og feiling eller bruke ein tabell for å kome fram til at svaret må vere 8 år.

Deretter kan du stille det andre spørsmålet, kor lang tid det vil ta før eit beløp er halvert dersom det minkar 10 % i verdi kvart år. Svaret på det skal vere 7 år.

Desse svara kan vere eit utgangspunkt for diskusjon. Er elevane overraska over at svara er ulike? Kvifor får dei ikkje same svar? Dersom vi endrar 10 % til eit anna tal, vil svara bli like då? Kan svara nokon gong bli like?

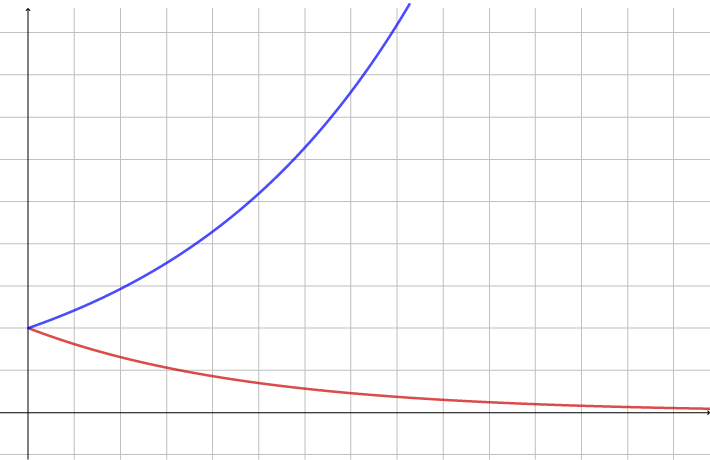
La elevane utforske, gjerne ved å prøve med fleire forskjellige prosentar. Det kan vere nyttig å bruke rekneark og/eller eit grafisk teikneprogram (f.eks. GeoGebra). Du kan oppfordre elevane til å representere problemet algebraisk. Grafisk bør dei sjå at grafane ikkje er like. Et viktig algebraisk poeng er at uttrykka ikkje er omvende eller motpartar (\(\frac12\) og 2 er motpartar, men \(1,1^x\) og \(0,9^x\) er ikkje det), og det fører til eit bevis for at svara aldri blir like.

Be elevane om å dele arbeidet sitt, og trekk fram og dra linjer mellom dei ulike representasjonane dei har brukt. Kan dei forklare kvifor dei to svara er ulike? Har nokon funne eit tal (ein prosent) som er slik at tida som trengst for dobling og halvering, blir lik? Eller har nokon greidd å bevise at dette er umogleg?

Gode rettleiingsspørsmål

• Er ein auke på 10 % det motsette av ein reduksjon på 10 %? Kva vil skje om du tek eit tal, aukar det med 10 % og reduserer det med 10 % etterpå?
• Er multiplisering med 1,1 det motsette av å multiplisere med 0,9? Kvifor?

Mogleg støtte

Dersom somme elevar ikkje kjenner multiplikasjonsmetoden for å rekne ut prosentvis auking eller reduksjon, kan det vere ein god idé å la dei bli kjende med denne metoden først.

For somme kan det vere vanskeleg å rekne ut prosentvis endring når det ikkje er oppgitt ein startverdi. I så fall kan dei kan velje ein startverdi og bruke han. Så kan dei endre startverdien og sjå om dei får det same resultatet. Deretter kan dei bruke ein valfri bokstav som startverdi (kan vere eit kva som helst tal) og sjå om dei framleis får det same resultatet. I resten av arbeidet kan du la elevane bruke ein bokstav som startverdi, eller eit valfritt tal (du kan f.eks. rå dei til å bruke 1 eller 100).