Lage bokser
Aktivitet
I denne aktiviteten begynner du med noen papirark med mål 15 x 15, og bruker dem til å lage små bokser.
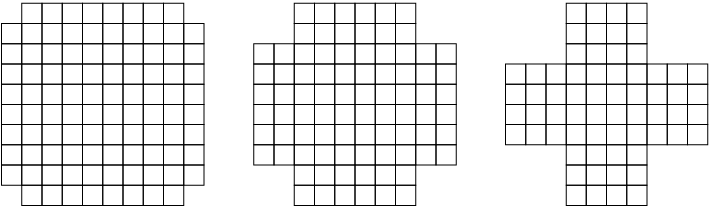
Du lager boksene ved å klippe ut kvadrater i hjørnene og brette opp sidene. De stiplede linjene på tegningen viser hvor du skal brette.
Begynn med å klippe ut et kvadrat i hvert hjørne. Brett opp sidene. Hva er størrelsen på grunnflaten? Hvor høye er sidene? Hva er volumet av boksen?
Klipp så ut et kvadrat med størrelse 2 x 2 i hvert hjørne, og brett opp sidene. Ser det ut som det er plass til mer enn, mindre enn eller like mye som i den første boksen? Hva er størrelsen på grunnflaten? Hvor høye er sidene nå? Hva er volumet?
Klipp så ut et kvadrat med størrelse 3 x 3 i hvert hjørne, og brett opp sidene. Ser det ut som det er plass til mer enn, mindre enn eller like mye som i den første boksen? Hva er størrelsen på grunnflaten? Hvor høye er sidene nå? Hva er volumet?
Hvis du fortsetter å gjøre dette, altså klippe bort større og større kvadrater i hjørnene, hvilken boks vil ha det største volumet?
Starthjelp
Hvor stor er grunnflaten/bunnen i boksen?
Hvor høye er sidene?
Hvor mye er det plass til i boksen?
Det kan være nyttig å skrive ut kvadratet under, som har målene 15 x 15.
Lærerveiledning
Hvorfor arbeide med denne oppgaven?
Denne aktiviteten kan brukes for å utvide elevenes ideer om areal. Den er også fin til å introdusere volum, selv om det er mulig å gjøre utforskingen uten å bruke ordet volum. Elevene visualisere boksene de lager, og noen kan bruke visualisering som hovedveien til en løsning. I tillegg er aktiviteten nyttig for å øve på gangetabellene, særlig kvadrattall.
Mulig tilnærming
Du kan begynne med å demonstrere hvordan man kan lage boksene (uten lokk) av et kvadrat på 10 x 10. Klipp først bort et lite kvadrat i hvert hjørne, og brett opp sidene.
Spør elevene hva arealet av grunnflaten er, og hvor mange kuber som får plass der. Hvordan vet de det? Nå skal du klippe bort et kvadrat på 2 x 2 i hvert hjørne, men før du gjør det, ber du dem om å se for seg hvordan boksen blir. Hva blir arealet av grunnflaten denne gangen, og hvor mange kuber får plass der? Du kan enten lage boksene så elevene får se, eller de kan sjekke visualiseringene sine. Fortsett med å klippe bort et kvadrat på 3 x 3 i hvert hjørne, og be elevene om å se for seg boksen. Du kan skrive ut et kvadrat på 10 x 10 fra kopioriginalen.
Presenter selve oppgaven, og gi elevene kvadratiske ark som de kan bruke til å arbeide med løsningene sine, gjerne i par, slik at de kan snakke sammen og diskutere ideer. De kan foreslå hvilken boks som vil ha det største volumet, og argumentere for forslaget sitt. Elevene må ha tilgang til saks og kanskje også teip.
Noen vil kanskje lage en tabell som viser resultatene, eller du kan skrive resultatene i klassen på tavla. Hvis dere fortsetter med kvadrater som er større og mindre enn 15, vil dere etter hvert se noen interessante tallmønstre.
La elevene vise fram arbeidet sitt, og diskuter resultatene i plenum. Var forslagene deres riktige? Hva legger de merke til med volumet når størrelsen på kvadratene som klippes bort, øker? Kan de tenke seg hvorfor det skjer?
Gode veiledningsspørsmål
- Hvor stor er grunnflaten/bunnen i denne boksen? Hvor høye er sidene? Hvor mye er det plass til?
- Er du sikker på at dette er et kvadrat? Tell og se.
- Hva skjer med volumet når vi klipper bort større og større kvadrater?
Mulig utvidelse
Elevene kan lage en graf som viser resultatene de fikk, eller de kan begynne med kvadrater i forskjellige størrelser. De som ikke trenger å lage mange bokser for å gjøre utregningene, kan klippe bort kvadrater på for eksempel 2,5 x 2,5 fra det store kvadratet.
Mulig støtte
Noen elever kan synes det er enklere å begynne med et kvadrat på 12 x 12. Da blir grunnflaten i den første boksen 10 x 10, som er et kjent starttall. Centikuber kan også være nyttige.
Ressursen er utviklet av NRICH