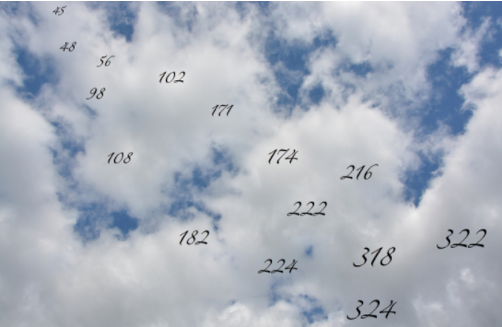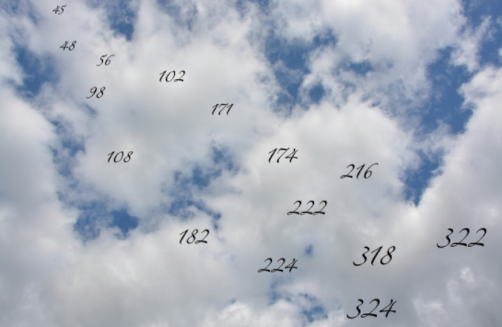Regnemester

Hvilke av tallene på bildet vil du komme til hvis du teller med seksere fra null? Hvordan vet du det?

Marius og Stine har funnet ut at de vil komme til 48, 102, 108, 174, 216, 222, 318 og 324. De syntes det var lett opp til 56, fordi de kan 6-gangen. Etterpå måtte de tenke og telle litt. De vet at 60 + 30 er 90, og at 90 er delelig med 6. Derfor kan ikke 98 være det. Videre vet de at 90 + 12 er 102, som de derfor må komme til (90 + 6 + 6), og at 108 er 6 mer enn 102. Så tok de 60 + 60 + 60 er 180. 180 - 6 er 174. De vil altså lande på 174, ikke på 171. De vil heller ikke lande på 182, som er 2 mer enn 180. 180 + 36 er 216. Både 180 og 36 er delelige med 6, og derfor vil de lande på 216. 222 er 6 mer enn 216, og de vil derfor lande der også. 224 vil de ikke lande på, for det er bare 2 mer enn 222. De vil ikke lande på 322, for det er 100 mer enn 222, og 100 er ikke delelig med 6. Både 300 og 18 er delelige med 6, og derfor vil de komme til 318. 324 er 6 mer enn 318, og de vil dermed komme dit også.

Isak og Even har følgende forklaring:

• Hvis 2 og 3 er faktorer til 6, må alle multipler av 6 være delelige med 2 og 3.
• Hvis et tall er en multippel av 2, er det et partall, altså vil det slutte på 0, 2, 4, 6 eller 8.
• For å avgjøre om et tall er en multippel av 3, kan vi legge sammen sifrene i tallet. Vi vet at hvis siffersummen er delelig med 3, er tallet delelig med 3.
• Eksempel: 108 er et partall. 1 + 0 + 8 = 9, og 9 er delelig med 3. Derfor er 108 delelig både med 2 og med 3, og vi vil komme til 108 hvis vi teller med seks fra null.
• Vi fant ut at vi kom til 102, 108, 174, 216, 222, 318 og 324.

Vil du komme til noen av disse tallene hvis du teller med sjuere fra null? Eventuelt hvilke? Hvordan vet du det?

Marius og Stine har brukt de samme strategiene som for steg med 6. De har funnet ut at de kommer til 56, 98, 224 og 322. De vet at de vil komme til 56, men ikke til noen av de andre tallene under 70. 70 + 28 er 98, og de vet at de vil komme dit. Da vet de at de ikke vil komme til 102 og 108. 70 + 70 er 140, og 171 er 31 mer enn 140. 31 er ikke delelig med 7, derfor vil de ikke komme til 171. 174 er 34 mer enn 140, og er heller ikke i sjugangen fordi 34 ikke er det. 182 er 42 større enn 140, og de kommer derfor til 182. 210 er delelig med 7, så de vil ikke komme til 216 eller 222, men 224 er 14 mer enn 210, og de vil komme dit. 224 + 100 er 324. De vet at 100 ikke er i sjugangen, og at de derfor ikke vil komme til 324. De har allerede funnet ut at 98 og 224 er i sjugangen. 98 + 224 er 322, og derfor vil de komme til 322, men ikke til 318 fordi det er bare 4 mindre enn 322.

Isak og Even har løst oppgaven på en helt annen måte:

• Ta det siste sifferet i tallet, doble det og subtraher fra det tallet som dannes av resten av sifrene. Hvis dette tallet er delelig med 7, vil starttallet være delelig med 7.
• Ta for eksempel 224. Det siste sifferet er 4, og hvis vi dobler det, får vi 8. Så subtraherer vi fra 22: 22 – 8 = 14. 14 er delelig med 7, og derfor er også 224 delelig med 7.
• Når vi brukte denne metoden, fant vi ut at vi kom til 224 og 322.

Kan du nå noen av disse tallene hvis du teller med niere fra null? Hvilke? Hvordan vet du det?

Isak og Even har også løst denne oppgaven med en regel:

• Vi kommer til å nå de tallene som er delelige med 9. For å finne ut om et tall er delelig med 9, legger vi sammen sifrene i tallet. Hvis tverrsummen er delelig med 9, er selve tallet også delelig med 9.
• Ta for eksempel 324. 3 + 2 + 4 = 9. 9 er delelig med 9, og derfor er også 324 delelig med 9.
• Tallene vi kommer til å nå, er 45, 108, 171, 216 og 324.

Vil du lande på noen av de samme tallene hvis du teller ned fra 350 med steg på 6? Hva med steg på 7 og 9? Hvordan vet du det?

Marius og Stine:

Vi startet på 350 og gikk med 6, 7 og 9 steg bakover. Hvis vi landet på det høyeste tallet som når vi startet på null, og gikk oppover, ville vi lande på de samme tallene. Hvis ikke ville vi aldri lande på de samme tallene. For seks steg var det største tallet 324. Da vi gikk bakover fra 350, traff vi ikke 324: 350 – 344 – 338 – 332 – 326 – 322. For sju steg var det største tallet 322. Det traff vi når vi gikk bakover: 350 – 343 – 336 – 329 – 322. Da vil vi også treffe alle de andre tallene for 7-stegene. For 9 steg var 324 det høyeste tallet. Vi startet igjen på 350: 350 – 341 – 332 – 323. Vi kommer ikke til å lande på noen av tallene for 9-stegene.

Isak og Even løste oppgaven slik:

• Vi kommer bare til å lande på de samme tallene hvis stegstørrelsen er en faktor til 350.
• Vi kan finne ut om stegstørrelsen er en faktor til 350 ved å bruke de samme metodene som vi brukte tidligere.
• 6 er ikke en faktor til 350. Tverrsummen er 3 + 5 + 0 = 8, og 8 er delelig med 2, men ikke med 3.
• 7 er en faktor til 350. Det siste sifferet er 0, og hvis vi dobler 0, får vi fortsatt 0. Det resterende sifferet er 35. 35 - 0 er 35, og 35 er delelig med 7.
• 9 er ikke en faktor til 350. Vi så for 350 at tverrsummen ikke er delelig med 3, og da kan den heller ikke være delelig med 9.
• Ved å bruke disse metodene fant vi ut at bare for 7 vil vi lande på de samme tallene.

Her er det andre bildet:

Marius og Stine sier: Vi kommer til å lande på tall som slutter på 00, 25, 50 eller 75 hvis vi teller med 25 om gangen. Da kommer vi til å lande på 175, 200, 350, 400, 650, 900 og 975.

For å finne ut hvilke tall vi kommer til å lande på hvis vi starter på 10 og teller med 25 om gangen, må vi legge på 10 på de to sluttsifrene fra forrige oppgave. Vi kommer til å lande på tall som slutter på 10, 35, 60 eller 85. Da kommer vi til å lande på 310 og 710.