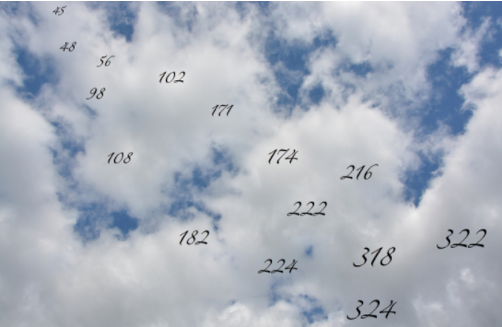Reknemeister

Kva for nokre av tala på biletet vil du kome til dersom du tel med seksarar frå null? Korleis veit du det?

Marius og Stine har funne ut at dei vil kome til 48, 102, 108, 174, 216, 222, 318 og 324. Dei syntest det var lett opp til 56, fordi dei kan seksgongen. Etter det måtte dei tenkje og telje litt. Dei veit at 60 + 30 er 90, og at 90 er deleleg med 6. Difor kan ikkje 98 vere det. Vidare veit dei at 90 + 12 er 102, som dei difor må kome til (90 + 6 + 6), og at 108 er 6 meir enn 102. Så tok dei 60 + 60 + 60 er 180. 180 – 6 er 174. Dei vil altså lande på 174, ikkje på 171. Dei vil heller ikkje lande på 182, som er 2 meir enn 180. 180 + 36 er 216. Både 180 og 36 er delelege med 6, og difor vil dei lande på 216. 222 er 6 meir enn 216, og dei vil difor lande der også. 224 vil dei ikkje lande på, for det er berre 2 meir enn 222. Dei vil ikkje lande på 322, for det er 100 meir enn 222, og 100 er ikkje deleleg med 6. Både 300 og 18 er delelege med 6, og difor vil dei kome til 318. 324 er 6 meir enn 318, og dei vil dermed kome dit også.

Isak og Even har denne forklaringa:

• Dersom 2 og 3 er faktorar av 6, må alle multiplar av 6 vere delelege med 2 og 3.
• Dersom eit tal er ein multippel av 2, er det eit partal, altså vil det slutte på 0, 2, 4, 6 eller 8.
• For å avgjere om eit tal er ein multippel av 3, kan vi leggje saman siffera i talet. Vi veit at dersom siffersummen er deleleg med 3, er talet deleleg med 3.
• Eksempel: 108 er eit partal. 1 + 0 + 8 = 9, og 9 er deleleg med 3. Difor er 108 deleleg både med 2 og med 3, og vi vil kome til 108 dersom vi tel med seks frå null.
• Vi fann ut at vi kom til 102, 108, 174, 216, 222, 318 og 324.

Vil du kome til nokre av desse tala dersom du tel med sjuarar frå null? Eventuelt kva tal? Korleis veit du det?

Marius og Stine har brukt dei same strategiane som for steg med 6. Dei har funne ut at dei kjem til 56, 98, 224 og 322. Dei veit at dei vil kome til 56, men ikkje til nokon av dei andre tala under 70. 70 + 28 er 98, og dei veit at dei vil kome dit. Då veit dei at dei ikkje vil kome til 102 og 108. 70 + 70 er 140, og 171 er 31 meir enn 140. 31 er ikkje deleleg med 7, difor vil dei ikkje kome til 171. 174 er 34 meir enn 140, og er heller ikkje i sjugongen, fordi 34 ikkje er det. 182 er 42 større enn 140, og dei kjem difor til 182. 210 er deleleg med 7, så dei vil ikkje kome til 216 eller 222, men 224 er 14 meir enn 210, og dei vil kome dit. 224 + 100 er 324. Dei veit at 100 ikkje er i sjugongen, og at dei difor ikkje vil kome til 324. Dei har alt funne ut at 98 og 224 er i sjugongen. 98 + 224 er 322, og difor vil dei kome til 322, men ikkje til 318, fordi det er berre 4 mindre enn 322.

Isak og Even har løyst oppgåva på ein heilt annan måte:

• Ta det siste sifferet i talet, doble det og subtraher dette frå det talet som blir laga av resten av siffera. Dersom dette talet er deleleg med 7, vil starttalet vere deleleg med 7.
• Ta for eksempel 224. Det siste sifferet er 4, og dersom vi doblar det, får vi 8. Så subtraherer vi 8 frå 22: 22 – 8 = 14. 14 er deleleg med 7, og difor er også 224 deleleg med 7.
• Når vi brukte denne metoden, kom vi til 224 og 322.

Kan du nå nokre av desse tala dersom du tel med niarar frå null? Kva tal? Korleis veit du det?

Isak og Even har også løyst denne oppgåva med ein regel:

• Vi kjem til å nå dei tala som er delelege med 9. For å finne ut om eit tal er deleleg med 9, legg vi saman siffera i talet. Dersom tverrsummen er deleleg med 9, er sjølve talet også deleleg med 9.
• Ta for eksempel 324. 3 + 2 + 4 = 9. 9 er deleleg med 9, og difor er også 324 deleleg med 9.
• Tala vi kjem til å nå, er 45, 108, 171, 216 og 324.

Vil du lande på nokre av dei same tala dersom du tel ned frå 350 med steg på 6? Kva med steg på 7 og 9? Korleis veit du det?

Marius og Stine tenkte slik:

Vi begynte på 350 og gjekk med 6, 7 og 9 steg bakover. Dersom vi landa på det høgaste talet som når vi begynte på null og gjekk oppover, ville vi lande på dei same tala. Dersom ikkje ville vi aldri lande på dei same tala. For seks steg var det største talet 324. Då vi gjekk bakover frå 350, trefte vi ikkje 324: 350 – 344 – 338 – 332 – 326 – 322. For sju steg var det største talet 322. Det trefte vi når vi gjekk bakover: 350 – 343 – 336 – 329 – 322. Då vil vi også treffe alle dei andre tala for 7-stega. For 9-stega var 324 det høgaste talet. Vi begynte igjen på 350: 350 – 341 – 332 – 323. Vi kjem ikkje til å lande på nokon av tala for 9-stega.

Isak og Even løyste oppgåva slik:

• Vi kjem berre til å lande på dei same tala dersom stegstorleiken er ein faktor til 350.
• Vi kan finne ut om stegstorleiken er ein faktor til 350 ved å bruke dei same metodane som vi brukte tidlegare.
• 6 er ikkje ein faktor til 350. Tverrsummen er 3 + 5 + 0 = 8, og 8 er deleleg med 2, men ikkje med 3.
• 7 er ein faktor til 350. Det siste sifferet er 0, og dersom vi doblar 0, får vi framleis 0. Resten av sifferet er 35. 35 – 0 er 35, og 35 er deleleg med 7.
• 9 er ikkje ein faktor til 350. Vi såg for 350 at tverrsummen ikkje er deleleg med 3, og då kan han heller ikkje vere deleleg med 9.
• Ved å bruke desse metodane fann vi ut at berre for 7 vil vi lande på dei same tala.

Her er det andre biletet:

Marius og Stine seier: Vi kjem til å lande på tal som sluttar på 00, 25, 50 eller 75, dersom vi tel med 25 om gongen. Då kjem vi til å lande på 175, 200, 350, 400, 650, 900 og 975.

For å finne ut kva tal vi kjem til å lande på dersom vi begynner på 10 og tel med 25 om gongen, må vi leggje 10 på dei to sluttsiffera frå den førre oppgåva. Vi kjem til å lande på tal som sluttar på 10, 35, 60 eller 85. Då kjem vi til å lande på 310 og 710.