Rett skal være rett
Problem
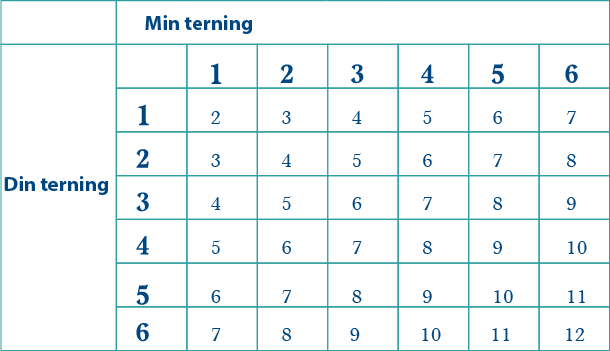
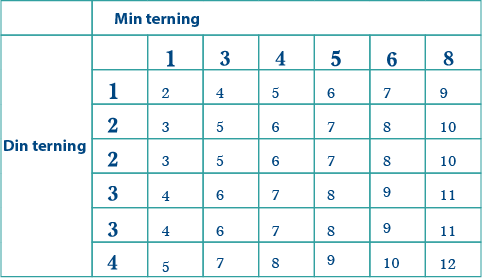
Denne tabellen viser mulige utfall når to vanlige terninger (min terning og din terning) trilles, og poengene på terningene legges sammen.
Du kan bruke tabellen til å se at sannsynligheten for å få 2 i sum er \(\frac1{36}\), sannsynligheten for å få 3 i sum er \(\frac2{36}\), sannsynligheten for å få 4 i sum er \(\frac3{36}\) osv.
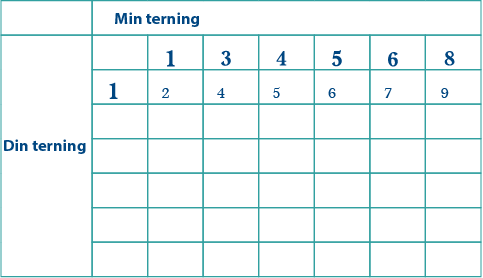
Se for deg at jeg endrer min terning ved å erstatte 2 med 8.
Kan du velge tall (øyne) på din terning slik at de to terningene gir nøyaktig samme sannsynlighet når de kastes? Det vil si at sannsynligheten for å få 2 i sum fortsatt skal være \(\frac1{36}\), sannsynligheten for å få 3 i sum fortsatt skal være \(\frac2{36}\), sannsynligheten for å få 4 sum fortsatt skal være \(\frac3{36}\) osv.?
Løsning
I tabellen som viser mulige poengsummer, trenger du én 2er, to 3ere, tre 4ere, fire 5ere, fem 6ere, seks 7ere, fem 8ere, fire 9ere, tre 10ere, to 11ere og én 12er.
Du kan ta i bruk tabeller og arbeide systematisk:
Du kan fylle ut tallene i din terning én rad om gangen. Du vet at du trenger én 2er, som må være summen av 1 + 1. Det betyr at du trenger én 1er på terningen din:
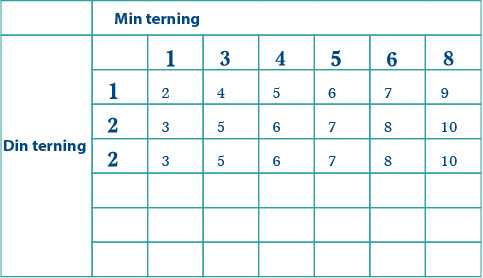
Du trenger også to 3ere. Den eneste måten du kan få 3 på er fra summen av min 1er og din 2er, siden min terning ikke har 2er. Det betyr at du trenger to 2ere på terningen din:
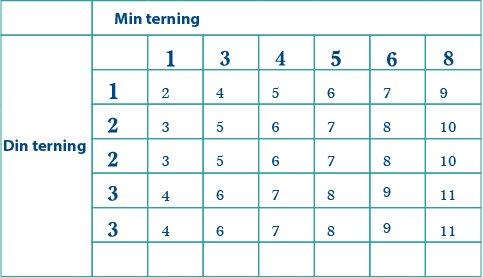
Du trenger også tre 4ere i sum, men så langt har du bare én, som kommer fra min 3er og din 1er. De andre må komme fra min 1er og din 3er. Du kan ikke putte flere 1ere på din terning, da ender du opp med for mange 2ere i sum. Det betyr at du trenger to 3ere på terningen din:
Hvilke andre summer mangler? Vi ser helt klart at 12 mangler i tabellen. 12 kan lages av min 8er og din 4er. Det betyr at du må ha én 4er på terningen din:
Om du teller over antallet til hver sum, vil du se at det stemmer!
Du kan også vurdere summer og arbeide deg logisk frem til en løsning:
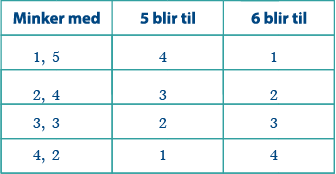
Når jeg endret min 2er til en 8er økte jeg den totale poengsummen på terningen min med 6 poeng. Om de to terningene skal «oppføre» seg som to normale terninger, kan ikke summene av de to terningene gå verken opp eller ned. Det betyr at du må minke den totale poengsummen på terningen din med 6 poeng.
Du vet at du ikke skal ha summer over 12, som betyr at du ikke kan ha 5 eller 6 på terningen din. Til sammen må din 5er og 6er reduseres med 6 poeng. Tabellen nedenfor viser de mulige reduksjonene som kan gjøres med 5 og 6, slik at den totale reduksjonen blir 6. Husk at verken 5 eller 6 kan reduseres til mindre enn 1, fordi det gjør det mulig å få en sum mindre enn 2.
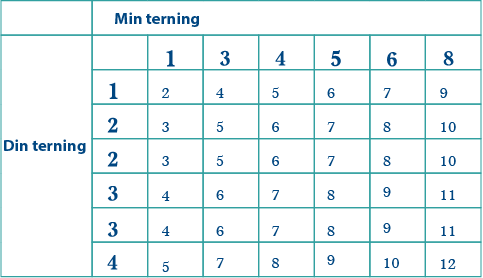
Tabellen viser at det er to mulige alternativer for terningen din: 1, 2, 3, 4, 4, 1, og 1, 2, 3, 4, 2, 3. Om du velger 1, 2, 3, 4, 4, 1, vil det være to mulige kombinasjoner som gir 2 som sum, og to mulige kombinasjoner som gi 12 som sum. Det er ikke lov, så den riktige kombinasjonen må være 1, 2, 3, 4, 2, 3. Om vi setter denne kombinasjonen inn i en tabell sammen med min terning, ser vi at det stemmer: