Rett skal vere rett
Problem
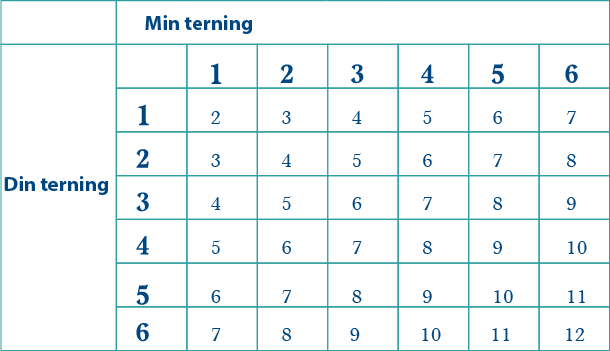
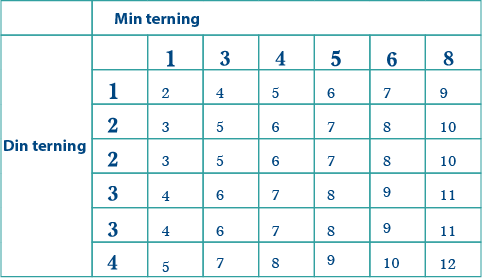
Denne tabellen viser moglege utfall når vi trillar to vanlege terningar (min terning og din terning), og legg saman poenga på terningane.
Du kan bruke tabellen til å sjå at sannsynet for at summen skal bli \(2\), er \(\frac1{36}\), sannsynet for at summen skal bli \(3\), er \(\frac2{36}\), sannsynet for at summen skal bli \(4\), er \(\frac3{36}\), osv.
Sjå for deg at eg endrar min terning ved å erstatte 2 med 8.
Kan du velje tal (auge) på din terning slik at dei to terningane gir nøyaktig same sannsyn når vi kastar dei? Det vil seie at sannsynet for at summen skal bli \(2\), framleis skal være \(\frac 1{36}\), sannsynet for at summen skal bli \(3\), framleis skal være \(\frac2{36}\), sannsynet for at summen skal bli \(4\), framleis skal være \(\frac3{36}\), osv.
Løysing
I tabellen som viser moglege poengsummar, treng du éin 2-ar, to 3-arar, tre 4-arar, fire 5-arar, fem 6-arar, seks 7-arar, fem 8-arar, fire 9-arar, tre 10-arar, to 11-arar og éin 12-ar.
Du kan ta i bruk tabellar og arbeide systematisk:
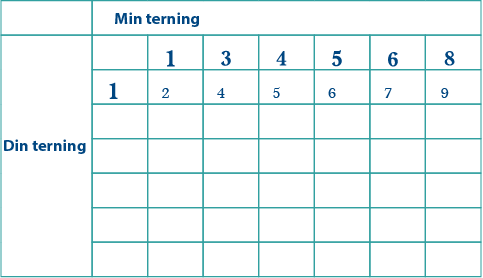
Fyll ut tala for din terning éi rad om gongen. Du veit at du treng éin 2-ar, som må vere summen av 1 + 1. Det betyr at du treng éin 1-ar på terningen din:
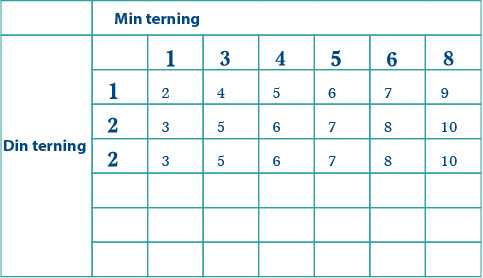
Du treng også to 3-arar. Den einaste måten du kan få 3 på, er frå summen av min 1-ar og din 2-ar, sidan min terning ikkje har 2-ar. Det betyr at du treng to 2-arar på terningen din:
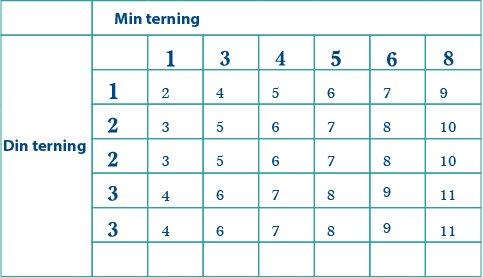
Du treng også tre 4-arar som sum, men så langt har du berre éin, som kjem frå min 3-ar og din 1-ar. Dei andre må kome frå min 1-ar og din 3-ar. Du kan ikkje putte fleire 1-arar på terningen din, då får du for mange 2-arar som sum. Det betyr at du treng to 3-arar på terningen din:
Kva for andre summar manglar? Vi ser heilt klart at 12 manglar i tabellen. 12 kan lagast av min 8-ar og din 4-ar. Det betyr at du må ha éin 4-ar på terningen din:
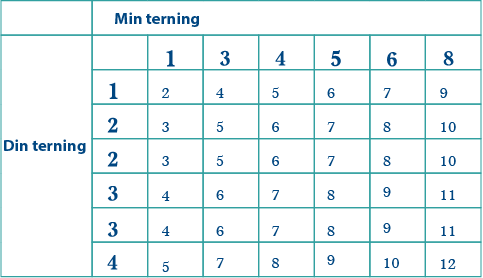
Dersom du tel over antalet til kvar sum, vil du sjå at det stemmer!
Du kan også vurdere summar og arbeide deg logisk fram til ei løysing:
Då eg endra 2-aren min til ein 8-ar, auka eg den totale poengsummen på terningen min med 6 poeng. Dersom dei to terningane skal «oppføre» seg som normale terningar, kan ikkje summane av dei to terningane gå verken opp eller ned. Det betyr at du må redusere den totale poengsummen på terningen din med 6 poeng.
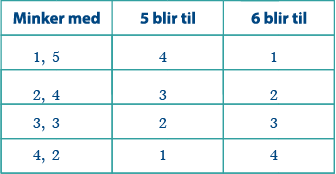
Du veit at du ikkje skal ha summar over 12, som betyr at du ikkje kan ha 5 eller 6 på terningen din. Til saman må 5-aren og 6-aren din reduserast med 6 poeng. Tabellen nedanfor viser dei moglege reduksjonane som kan gjerast med 5 og 6, slik at den totale reduksjonen blir 6. Hugs at verken 5 eller 6 kan reduserast til mindre enn 1, fordi då blir det mogleg å få ein sum mindre enn 2.
Tabellen viser at det er to moglege alternativ for terningen din: 1, 2, 3, 4, 4, 1, og 1, 2, 3, 4, 2, 3. Dersom du vel 1, 2, 3, 4, 4, 1, vil det vere to moglege kombinasjonar som gir 2 som sum, og to moglege kombinasjonar som gi 12 som sum. Det er ikkje lov, så den rette kombinasjonen må vere 1, 2, 3, 4, 2, 3. Når vi set denne kombinasjonen inn i ein tabell saman med terningen min, ser vi at det stemmer: