Fjern et tall
Aktivitet
Du har tallene 1, 2, 3, 4, 5, 6. Velg ett tall som du fjerner fra de andre.
Du kan for eksempel fjerne 5, slik at det står igjen 1, 2, 3, 4, 6.
Gjennomsnittet av disse tallene er 3,2.
- Kan du fjerne ett av de andre tallene fra 1 til 6, slik at gjennomsnittet blir et heltall?
Du har tallene fra 1 til N, der N er et partall. Så fjerner du ett tall og finner gjennomsnittet.
- Hvilke tall kan du fjerne av de N tallene slik at gjennomsnittet blir et heltall? Kan du forklare hvorfor det blir slik?
Hvordan blir det hvis N er et oddetall?
Her er noen flere oppgaver som du kan prøve deg på:
- Ett av tallene 1, 2, 3, 4, 5, 6 er fjernet, og gjennomsnittet av tallene som står igjen, er 3,6. Hvilket tall er fjernet?
- Ett av tallene fra 1 til 15 er fjernet, og gjennomsnittet av tallene som står igjen, er \(7,\dot{7}1428\dot{5}\) (desimalene 714285 gjentas i det uendelige). Hvilket tall er fjernet?
- Ett av tallene fra 1 til N, der N er et ukjent tall, er fjernet. Gjennomsnittet av tallene som står igjen, er \(6,8\dot{3}\) (desimalen 3 gjentas i det uendelige). Hvilket tall er N, og hvilket tall er fjernet?
- Ett av tallene fra 1 til N er fjernet, og gjennomsnittet av tallene som står igjen, er 25,76. Hvilket tall er N, og hvilket tall er fjernet?
Starthjelp
- Hvordan regner vi ut gjennomsnittet av en gruppe tall?
- Når du fjerner ett av tallene fra 1 til 6, hvilket tall må da gå opp i summen av tallene hvis gjennomsnittet skal bli et helt tall?
- Hvis du vet hvor mange tall du har, og hva gjennomsnittet av disse tallene er, hva vet du da om summen av tallene?
Løsning
Vi begynner med tallene 1, 2, 3, 4, 5, 6. Når vi stryker ett tall, blir det 5 tall igjen. Gjennomsnittet er summen av tallene delt på antall tall. Når vi stryker ett av tallene, skal vi dele på 5. Det betyr at summen må være et tall i 5-gangen, hvis gjennomsnittet skal bli et helt tall. Tallene som er mindre enn 5, kan vi gruppere i to par som begge blir 5 til sammen: 1 + 4 = 5, og 2 + 3 = 5. Hvis vi stryker 6, blir summen 15 og gjennomsnittet 15 : 5 = 3. Legger vi sammen tallene fra 1 til 6, får vi 21, 1 mer enn 20, som 5 går opp i. Så hvis vi stryker 1, blir gjennomsnittet 20 : 5 = 4.
Hvis vi har tallene 1, 2, 3, 4, 5, 6, 7, 8, kan vi tenke på samme måte. Når vi stryker ett tall, har vi 7 igjen. Tallene som er mindre enn 7, kan vi gruppere i par som blir 7 til sammen: 1 + 6 = 7, 2 + 5 = 7 og 3 + 4 = 7. Hvis vi stryker 8, blir summen 28 og gjennomsnittet 28 : 7 = 4. Vi kan også velge å beholde 8 og stryke 1. Da får vi også en sum som er delelig på 7, og gjennomsnittet blir et helt tall, 35 : 7 = 5.
Hvis vi lar N være et partall og har tallene 1, 2, 3, …, N, kan vi resonnere på samme måte. Av alle tallene som er mindre enn N – 1, kan vi lage par som blir N – 1 til sammen. Så hvis vi fjerner N, er summen et helt tall multiplisert med N – 1. Hvis vi fjerner 1 og legger til N, har summen økt med N – 1.
For at gjennomsnittet skal bli et helt tall, kan vi altså stryke 1 eller N når N er et partall.
Det er ingen andre tall vi kan stryke, for når vi fjerner det minste tallet, 1, blir gjennomsnittet \(\frac{N}2+1\), og hvis vi fjerner det største tallet, N, blir gjennomsnittet \(\frac{N}2\). Hvis vi hadde fjernet et tall mellom 1 og N, måtte gjennomsnittet vært et tall mellom disse to, men det finnes ikke noe helt tall mellom to påfølgende heltall.
Hvis vi lar N være et oddetall, blir det annerledes.
Hvis vi har tallene 1, 2, 3, blir gjennomsnittet et helt tall når vi stryker 2.
Hvis vi har tallene 1, 2, 3, 4, 5, blir gjennomsnittet et helt tall når vi stryker 3.
Hvis vi har tallene 1, 2, 3, 4, 5, 6, 7, blir gjennomsnittet et helt tall når vi stryker 4.
Hvis vi har tallene 1, 2, 3, 4, 5, 6, 7, 8, 9, blir gjennomsnittet et helt tall når vi stryker 5.
Det ser ut til at hvis N er et oddetall og vi stryker \(\frac{N+1}2\) (medianen), vil gjennomsnittet bli et helt tall. Når N er et oddetall og vi fjerner et tall, finner vi gjennomsnittet ved å dele på N – 1, som er et partall.
En måte å forklare det på er slik:
Vi lar N være et oddetall og tenker oss at vi har tallene 1, 2, 3, …, N. Summen av de N første naturlige tallene er \(\frac{(N+1)N}2\).
Vi ser hva vi får igjen hvis vi trekker fra \(\frac{N+1}2\):
\(\begin{align} \frac{(N+1)N}2-\frac{N+1}2&=\\ \frac{N^2+N-N-1}2&=\\ \frac{N^2-1}2&=\\ \frac{(N+1)(N-1)}2&=\\ \frac{N+1}2\cdot(N-1) \end{align}\)
\(\frac{N+1}2\) er et helt tall, siden N er et oddetall. Så hvis vi trekker medianen, \(\frac{N+1}2\), fra summen av alle de N tallene, blir summen et helt tall multiplisert med N – 1. Da vet vi at om vi dividerer summen av de resterende tallene på N – 1, blir gjennomsnittet et helt tall.
Det finnes ingen flere muligheter, for gjennomsnittet må ligge mellom \(\frac{N}2\) og \(\frac{N}2+1\), og det eneste hele tallet mellom de to er \(\frac{N+1}2\).
I lærerveiledningen finnes det visuelle bevis (bevis ved figurer) for disse sammenhengene.
Ekstra utfordringer
- Ett av tallene 1, 2, 3, 4, 5, 6 blir fjernet, og gjennomsnittet av tallene som står igjen, er 3,6. Hvilket tall er fjernet?
Løsning:
Hvis gjennomsnittet av 5 tall er 3,6, er summen av de fem tallene \(5\cdot3,6=18\). Summen av de hele tallene fra 1 og oppover er trekanttallene, og det sjette trekanttallet (\(1+2+3+4+5+6\)) er 21. Da må det være 3-tallet som er fjernet, siden \(21-18=3\).
- Ett av tallene fra 1 til 15 er fjernet, og gjennomsnittet av tallene som står igjen, er \(7,\dot{7}1428\dot{5}\) (desimalene 714285 gjentas i det uendelige). Hvilket tall er fjernet?
Løsning:
Summen av de 15 første heltallene er \(\frac{1+15}2\cdot15=120\).
Vi skal trekke fra et ukjent tall x og finne gjennomsnittet av de 14 gjenværende tallene:
\(\begin{align}\frac{120-x}{14}&=7,714285714285\\ 120 - x &= 14\cdot7,714285714285\\ 120-x&=108\\ x&=12 \end{align}\)
Tallet 12 er fjernet.
- Ett av tallene fra 1 til N, der N er et ukjent tall, er fjernet. Gjennomsnittet av tallene som står igjen, er \(6,8\dot{3}\) (desimalen 3 gjentas i det uendelige). Hvilket tall er N, og hvilket tall er fjernet?
Løsning:
Gjennomsnittstallet av flere påfølgende heltall ligger «midt i» tallene når de står i rekkefølge. Hvis gjennomsnittet av noen påfølgende heltall er 6,8333…, kan vi gjette at det største tallet må være 13 eller 14. (Gjennomsnittet av heltallene 1–12 er 6,5, og av 1–13 er det 7.) Siden 3 gjentas i desimalene, antar vi at antallet som summen er delt på, må ha 3 som faktor. I dette tilfellet er det 12. Da er det største tallet 13, og tallet som er tatt bort, er x:
\(1+2+3+...+13=\frac{1+13}2\cdot13= 91\\ \begin{align} \frac{91-x}{12}&=6,8\dot3\\ -(-x)&=-(6,8\dot3\cdot12-91)\\ x&\approx9 \end{align}\)
N = 13, og 9 er fjernet.
- Ett av tallene fra 1 til N er fjernet, og gjennomsnittet av tallene som står igjen, er 25,76. Hvilket tall er N, og hvilket tall er fjernet?
Løsning:
Gjennomsnittet av heltallene 1–50 er 25,5, og av 1–51 er det 26. Da kan vi anta at N er 51 eller 52. Siden gjennomsnittet er et desimaltall med et endelig antall desimaler, antar vi at N = 51, slik at vi skal dele summen av alle tallene på partallet 50:
\(1+2+3+...+51=\frac{51+1}2\cdot51=1326\\ \\ \begin{align} \frac{1326-x}{50}&=26,76\\ x&=-(26,76\cdot50-1326)\\ x&=38 \end{align}\)
N = 51, og 38 er fjernet.
Lærerveiledning
Hvorfor arbeide med denne oppgaven?
Ved å arbeide med dette problemet får elevene utviklet forståelsen av hva et gjennomsnitt er. De må dessuten resonnere, generalisere, argumentere og forklare.
Mulig tilnærming
Begynn med å si at alle skal skrive de hele tallene fra 1 til 6, stryke ut ett og finne gjennomsnittet av resten. Når alle har gjort det, kan de fortelle hvilket tall de har strøket, og hva gjennomsnittet ble. Det blir mange ulike svar, og noen har kanskje fått et helt tall til svar. Kommenter at det er interessant at to (eller en eller flere) har fått et helt tall som svar. Hvis ingen har fått et heltallig svar, må du kommentere det.
Nå skal elevene undersøke mulige gjennomsnitt hvis de har N heltall fra 1 og oppover, og stryker ett av dem. Presiser at N skal være et partall.
- Vil det alltid være mulig å stryke et tall og få et helt tall som gjennomsnitt?
- Kan det gjøres på mer enn én måte?
Elevene må få undersøke flere partall før dere generaliserer. Du vil kanskje gi ulike elevpar ulike partall å undersøke, eller de kan velge de partallene de selv vil undersøke. Når alle har fått undersøkt sine tall, samles hele klassen. La elvene fortelle og forklare, lytte til hverandres forklaringer og sammenligne. Har de kommet fram til like løsninger eller ikke?
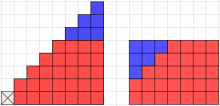
Det finnes mange måter å vise at gjennomsnittet, når N er partall, blir et helt tall hvis vi fjerner 1 eller N. I løsningsforslaget har vi begynt med noen talleksempler og så vist det algebraisk. Det kan også vises visuelt. Så snart vi har fjernet 1 eller N, er antall tall et oddetall. Gjennomsnittet av disse tallene vil bli lik det midterste tallet.
Selv om disse figurene viser tilfellet med N = 8, viser de noe som gjelder for alle partall N. Hvis vi tar bort 1, blir gjennomsnittet \(\frac{N}2+1\), og hvis vi tar bort N, blir gjennomsnittet \(\frac{N}2\). Da er det ikke flere heltallige løsninger.
Klassen må få tid til å forstå hva figurene viser. Hva illustrerer figuren som ser ut som en trapp? Hvorfor sier vi at gjennomsnittet er et helt tall, hvis vi kan «bygge om» tallene slik at vi får et rektangel? Hvilket tall eller hvilken side i rektangelet er fast hvis det skal illustrere gjennomsnittet av tallene? Hva representerer høyden på rektangelet? Finnes måter å fjerne andre tall på slik at vi får rektangler med samme lengde, men andre høyder?
Når elevene har blitt fortrolige med dette beviset, kan de undersøke tilfeller der N er oddetall. La dem undersøke flere eksempler, og utfordre dem til å prøve å finne en generell løsning: Vi vi alltid få et heltallig gjennomsnitt hvis vi fjerner ett tall i en følge på 1 – N naturlige tall når N er et oddetall? Finnes det flere måter å gjøre det på?
Elevene kan gjerne lage et visuelt bevis for løsningen. Kan de forklare hva de tegner, og hvorfor? Kan de argumentere for at det er bare hvis vi fjerner det midterste tallet, at gjennomsnittet blir et helt tall?
Gode veiledningsspørsmål
Til ekstraspørsmålene til slutt i opplegget:
- Hvis du kjenner gjennomsnittet av noen tall, og du vet hvor mange tall det er, hva vet du da om summen av tallene?
- Hvis du kjenner gjennomsnittet av noen heltall fra 1 og oppover, hvor mange tall er det da mulig at det største heltallet kan være?
- Hvis gjennomsnittet har desimaler som gjentas i det uendelige, hvordan kan det hjelpe deg til å finne hvilket tall en må ha dividert med?
Mulig utvidelse
Hva blir gjennomsnittet hvis vi fjerner ett tall fra for eksempel disse følgene:
- 71, 72, 73, 74, 75, 76
- 2, 4, 6, 8, 10
- 1000, 1004, 1008, 1012, 1016
Mulig støtte
Elevene kan arbeide med oppgavene G, T og M og Ulike sentralmål først.
Ressursen er utviklet av NRICH