Fjern eit tal

Kvifor arbeide med denne oppgåva?

Ved å arbeide med dette problemet får elevane utvikla forståinga av kva eit gjennomsnitt er. Dei må dessutan resonnere, generalisere, argumentere og forklare.

Mogleg tilnærming

Begynn med å seie at alle skal skrive dei heile tala frå 1 til 6, stryke ut eitt og finne gjennomsnittet av resten. Når alle har gjort det, kan dei fortelje kva tal dei har stroke, og kva gjennomsnittet vart. Det blir mange ulike svar, og nokon har kanskje fått eit heilt tal til svar. Kommenter at det er interessant at to (eller ein eller fleire) har fått eit heilt tal som svar. Viss ingen har fått eit heiltalig svar, må du kommentere det.

No skal elevane undersøkje moglege gjennomsnitt viss dei har N heiltal frå 1 og oppover, og stryk eitt av dei. Presiser at N skal vere eit partal.

Vil det alltid vere mogleg å stryke eit tal og få eit heilt tal som gjennomsnitt?

Kan det gjerast på meir enn éin måte?

Elevane må få undersøkje fleire partal før de generaliserer. Du vil kanskje gi ulike elevpar ulike partal å undersøkje, eller dei kan velje dei partala dei sjølv vil undersøkje. Når alle har fått undersøkt tala sine, samlast heile klassen. La elvane fortelje og forklare, lytte til forklaringane til kvarandre og samanlikne. Har dei komme fram til like løysingar eller ikkje?

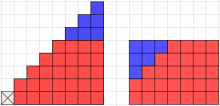
Det finst mange måtar å vise at gjennomsnittet, når N er partal, blir eit heilt tal viss vi fjernar 1 eller N. Så snart vi har fjerna 1 eller N, er talet på tal eit oddetal. Gjennomsnittet av desse tala vil bli lik det midtarste talet.

Sjølv om desse figurane viser tilfellet med N = 8, viser dei noko som gjeld for alle partal N. Viss vi tek bort 1, blir gjennomsnittet  \(\frac{N}2+1\), og viss vi tek bort N, blir gjennomsnittet \(\frac{N}2\). Då er det ikkje fleire heiltalige løysingar.

Klassen må få tid til å forstå kva figurane viser. Kva illustrerer figuren som ser ut som ei trapp? Kvifor seier vi at gjennomsnittet er eit heilt tal, viss vi kan «byggje om» tala slik at vi får eit rektangel? Kva tal eller kva side i rektangelet er fast viss det skal illustrere gjennomsnittet av tala? Kva representerer høgda på rektangelet? Finnes det måtar å fjerne andre tal på slik at vi får rektangel med same lengd, men andre høgder?

Når elevane har vorte fortrulege med dette beviset, kan dei undersøkje tilfelle der N er oddetal. La dei undersøkje fleire døme, og utfordre dei til å prøve å finne ei generell løysing: Vil vi alltid få eit heiltalig gjennomsnitt viss vi fjernar eitt tal i ei følgje på 1 – N naturlege tal når N er eit oddetal? Finst det fleire måtar å gjere det på?

Elevane kan gjerne lage eit visuelt bevis for løysinga. Kan dei forklare kva dei teiknar, og kvifor? Kan dei argumentere for at det er berre viss vi fjernar det midtarste talet, at gjennomsnittet blir eit heilt tal?

Gode rettleiingsspørsmål

Til ekstraspørsmåla til slutt i opplegget:

• Viss du kjenner gjennomsnittet av nokon tal, og du veit kor mange tal det er, kva veit du då om summen av tala?
• Viss du kjenner gjennomsnittet av nokon heiltal frå 1 og oppover, kor mange tal er det då mogleg at det største heiltalet kan vere?
• Viss gjennomsnittet har desimalar som blir gjentekne i det uendelege, korleis kan det hjelpe deg til å finne kva tal ein må ha dividert med?

Mogleg utviding

Kva blir gjennomsnittet viss vi fjernar eitt tal frå til dømes desse følgjene:

71, 72, 73, 74, 75, 76

2, 4, 6, 8, 10

1000, 1004, 1008, 1012, 1016

Mogleg støtte

Elevane kan arbeide med oppgåvene G, T og M og Ulike sentralmål først.