Fire lys
Aktivitet
Fire lys skal plasseres i et mønster på et flatt bord på en sånn måte at det bare kan være to forskjellige avstander mellom lysene.
Tegn og forklar hvordan lysene kan plasseres, på en måte som gjør at andre elever skal kunne lese og forstå hvordan du har tenkt.
Tegn en skisse av alle løsningene.
Løsning
Det er mange måter å løse dette på. Her er noen eksempler.
Eksempel 1:
Dette er kanskje den enkleste løsningen.
Eksempel 2:
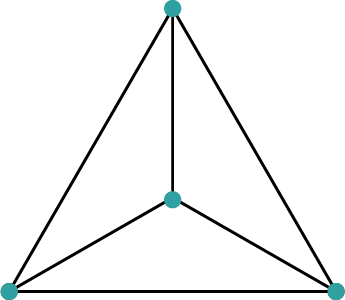
Plasser et lys i hvert hjørne av en likesidet trekant, og det fjerde lyset i sentrum av den omskrevne sirkelen.
Dette gir riktig løsning, fordi sentrum av den omskrevne sirkelen ligger i skjæringspunktet mellom midtnormalene til sidene i trekanten.
Eksempel 3 og 4:
Plasser et lys i hvert hjørne av en likesidet trekant, og det fjerde lyset på forlengelsen av høyden fra et hjørne ned på motstående sidekant på to måter:
Eksempel 5:
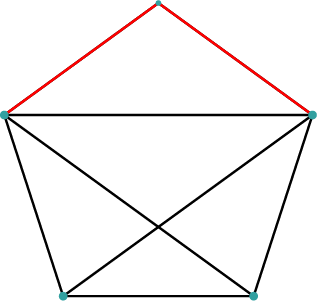
Plasser et lys i fire hjørner av en regulær femkant:
Tre av avstandene er diagonaler i femkanten, og de tre andre er sidekanter i femkanten.
Eksempel på løsning som ikke blir helt riktig:
Plasser et lys i hvert hjørne av en likesidet trekant og det fjerde lyset der høyden fra et hjørne treffer grunnlinja.
Her blir det tre forskjellige avstander mellom lysene.
Lærerveiledning
Hva ønsker vi med denne aktiviteten?
Oppgaven kan utvikle elevenes forståelse av geometri. Elevene skal bruke kunnskaper de har om geometriske former til å få dypere innsikt i avstander mellom punkter og linjer i figurene. De skal videre få øvelse i å lage skisser, konstruere med passer og linjal, og eventuelt tegne figurene i GeoGebra.
Mulig tilnærming
Introduser oppgaven muntlig. Åpne for spørsmål hvis noe er uklart for elevene. Det kan være lurt å presisere at hvis to løsninger er formlike, skal de telle som like løsninger. Elevene kan utforske problemet på egen hånd eller i små grupper (2–4 elever). Forbered dem på at de skal presentere svarene sine, og utfordre dem til å argumentere for løsningene sine.
Observer elevene mens de arbeider med oppgaven. Oppmuntre dem til å diskutere mulige løsninger med hverandre, og til å begrunne hvorfor løsningene oppfyller kravene som er gitt i oppgaven.
Observer gruppenes arbeid underveis. Legg merke til hvordan de diskuterer problemet, og hvilke løsninger de kommer fram til. Velg en god rekkefølge for presentasjonen, og la gruppene vise fram løsningene i denne rekkefølgen. Elevene kan tegne skisser på tavla. Ta også fram løsninger som ikke er riktige. Uten å si hvilke som er riktige eller gale, ber du elevene diskutere om de ulike forslagene tilfredsstiller kravene i oppgaven. Klassen kommer fram til korrekte løsninger sammen.
Som avslutning på undervisningsøkta kan elevene skrive et geometrisk begrep de har brukt i løpet av økta, og en presis definisjon av dette begrepet på en «gul-lapp». «Gul-lappen» klistrer på døra før de går.
Gode veiledningsspørsmål
Vær litt gnien med veiledningsspørsmålene. La elevene streve før du stiller dem.
- Hvordan kan dere begynne, og hvorfor?
- Hvor mange ulike lengder er det i denne figuren?
- Hvorfor oppfyller denne figuren alle kravene i oppgaven?
- Hvordan beholder dere god oversikt over det dere har funnet ut?
Mulig utvidelse
Vis at løsningene er riktige ved å konstruere figurene som framkommer ved hjelp av passer og linjal. Tegn figurene som framkommer, i GeoGebra.
Mulig støtte
Diskuter løsningsforslag som elevene kommer med, og pek på hva som gjør at figuren fyller / ikke fyller kravene i oppgaven.
Ressursen er utviklet av Matematikksenteret