Fire lys
Aktivitet
Fire lys skal plasserast i eit mønster på eit flatt bord på ein slik måte at det berre kan vere to forskjellige avstandar mellom lysa.
Teikn og forklar korleis lysa kan plasserast, på ein måte som gjer at andre elevar skal kunne lese og forstå korleis du har tenkt.
Teikn ei skisse av alle løysingane.
Løysing
Det er mange måtar å løyse dette på. Her er nokre eksempel.
Eksempel 1:
Dette er kanskje den enklaste løysinga.
Eksempel 2:
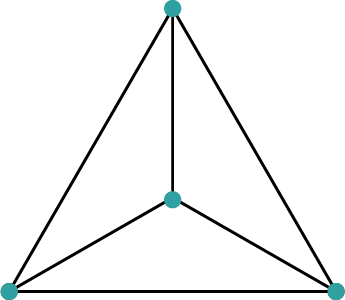
Plasser eit lys i kvart hjørne av ein likesida trekant, og det fjerde lyset i sentrum av den omskrivne sirkelen.
Det gir rett løysing, fordi sentrum i den omskrivne sirkelen ligg i skjeringspunktet mellom midtnormalane på sidene i trekanten.
Eksempel 3 og 4:
Plasser eit lys i kvart hjørne av ein likesida trekant, og det fjerde lyset på forlenginga av høgda frå eit hjørne ned på den motståande sidekanten på to måtar:
Eksempel 5:
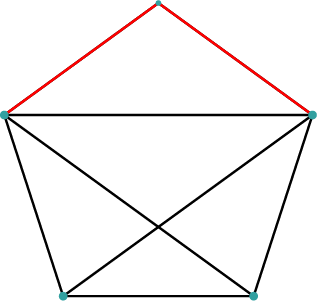
Plasser eit lys i fire hjørne av ein regulær femkant:
Tre av avstandane er diagonalar i femkanten, og dei tre andre er sidekantar i femkanten.
Eksempel på ei løysing som ikkje er heilt rett:
Plasser eit lys i kvart hjørne av ein likesida trekant og det fjerde lyset der høgda frå eit hjørne treffer grunnlinja.
Her blir det tre forskjellige avstandar mellom lysa.
Lærarrettleiing
Kvifor arbeide med denne oppgåva?
Oppgåva kan utvikle forståinga av geometri hos elevane. Dei skal bruke kunnskapar dei har om geometriske former til å få djupare innsikt i avstandar mellom punkt og linjer i figurane. Dei skal også få øving i å lage skisser, konstruere med passar og linjal, og eventuelt teikne figurane i GeoGebra.
Mogleg tilnærming
Introduser oppgåva munnleg. Opne for spørsmål dersom noko er uklart for elevane. Det kan vere lurt å presisere at dersom to løysingar er formlike, skal dei telje som like løysingar. Elevane kan utforske problemet på eiga hand eller i små grupper (2–4 elevar). Førebu dei på at dei skal presentere svara sine og argumentere for løysingane sine.
Observer elevane medan dei arbeider med oppgåva. Oppmuntre dei til å diskutere moglege løysingar med kvarandre, og til å grunngi kvifor løysingane oppfyller krava i oppgåva.
Observer arbeidet i gruppene undervegs. Legg merke til korleis dei diskuterer problemet, og kva for løysingar dei kjem fram til. Vel ei god rekkjefølgje for presentasjonen, og la gruppene vise fram løysingane i denne rekkjefølgja. Elevane kan teikne skisser på tavla. Trekk også fram løysingar som ikkje er rette. Utan å seie kva for nokre som er rette eller feil, ber du elevane diskutere om dei ulike forslaga tilfredsstiller krava i oppgåva. Klassen kjem fram til korrekte løysingar saman.
Som avslutning på undervisningsøkta kan elevane skrive eit geometrisk omgrep dei har brukt denne økta, og ein presis definisjon av dette omgrepet på ein post-it-lapp. Lappen klistrar dei på døra før dei går.
Gode rettleiingsspørsmål
Ver litt sparsam med rettleiingsspørsmåla. La elevane streve før du stiller dei.
- Korleis kan de begynne, og kvifor?
- Kor mange ulike lengder er det i denne figuren?
- Kvifor oppfyller denne figuren alle krava i oppgåva?
- Korleis kan de halde god oversikt over det de har funne ut?
Mogleg utviding
Vis at løysingane er rette ved å konstruere figurane som kjem fram ved hjelp av passar og linjal. Teikn figurane som kjem fram, i GeoGebra.
Mogleg støtte
Diskuter løysingsforslag som elevane kjem med, og peik på det som gjer at figuren oppfyller eller ikkje oppfyller krava i oppgåva.
Ressursen er utviklet av Matematikksenteret