Småkaker i boksen
Aktivitet
Lisa, Nicolai og Mattias var på overnattingsbesøk hos bestefar og bestemor. Der var det en boks med mange kaker. Barnebarna skulle få kaker dagen etter.
Da Lisa hadde lagt seg, klarte ikke Nicolai å vente lenger. Han fant kakeboksen og tok \(\frac15\) av kakene. Før Mattias skulle legge seg tok han \(\frac14\) av kakene som da var i boksen. Lille Lisa var tidlig oppe og tok to kaker. Da bestemor kom, så hun at det bare var 22 kaker igjen.
Hvor mange kaker hadde det vært i boksen?
Tilleggsspørsmål:
Bestemor hadde egentlig tenkt at siden Mattias var eldst så skulle han få \( {1\over 4}\) av alle kakene. Nicolai skulle få \( {1\over 5}\) av alle kakene, og lille Lisa skulle få to kaker.
Tok de tre barnebarna så mange småkaker som bestemor hadde planlagt at de skulle få? Begrunn svaret!
Løsning
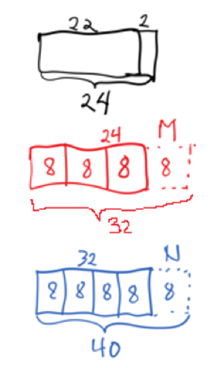
Lille Lisa får 2 kaker, før hun forsynte seg var det 24 kaker.
Dette er \( {3 \over 4}\) av de kakene som var i boksen før Mattias forsynte seg med \( {1 \over 4}\). Før Mattias forsynte seg var det derfor 32 kaker i boksen, og Mattias tok 8 kaker.
De 32 kakene er \( {4 \over 5}\) av de kakene som var i boksen før Nicolai forsynte seg med sin del.
Det vil si at det var 40 kaker i boksen før barnebarna kom på besøk, og Nicolai tok 8 kaker.
Lærerveiledning
Hvorfor arbeide med denne oppgaven?
Hensikten med aktiviteten er å arbeide med problemløsingsstrategier. Oppgaven inviterer elevene til å ta i bruk strategien Tenke baklengs. Elevene blir presentert for et problem, der utgangspunktet er ukjent, hvor det vil være naturlig å tenke baklengs. De fleste starter med den informasjonen som er kjent, og den står i slutten av teksten. Elevene må analysere konteksten, reflektere over hva som har skjedd underveis og hvilken regneart som beskriver hendelsen. Hver gang småkaker forsvinner fra kakeboksen beskrives det ved hjelp av subtraksjon, og når de skal gå bakover i tid og beskrive den motsatte hendelsen må de bruke addisjon. Å forstå at regnearten blir motsatt når de arbeider baklengs er avgjørende når man bruker strategien å tenke baklengs. Antall kaker som ble tatt (subtraksjon), må legges til når de arbeider baklengs (addisjon).
Det matematiske målet med aktiviteten er å utforske egenskaper ved brøk som del av hel. Elevene må vite at brøkdelene av samme helhet må være like store. De får erfaring med at helheten kan variere, og at to ulike brøker kan utgjøre samme mengde eller antall når helhetene de regnes av er forskjellige. Elevene er ofte flinke til å regne brøkdelen av en hel (mengde), men får problemer når de skal gå motsatt vei og finne helheten.
Mulig tilnærming
Du kan presentere oppgaven som en fortelling for elevene. Elevene kommer med forslag i plenum om hvordan de vil starte arbeidet med problemet. Når elevene starter arbeidet med problemet, får de utdelt oppgaven skriftlig i tillegg til plastbrikker de kan bruke om de ønsker det.
Denne oppgaven egner seg fint som gruppeoppgave og legger til rette for gode matematiske samtaler. Oppfordre gjerne gruppene til å uttrykke løsningsforslagene sine både muntlig og skriftlig.
Elevene vil kunne løse denne oppgaven på mange ulike måter og med ulike strategier. De vil kunne:
- Ta utgangspunkt i et mer eller mindre tilfeldig tall, sjekke om det blir 22 til slutt.
- Ta utgangspunkt i 5 - gangen, fordi Nicolai skal ha en femdel.
Elever som tar utgangspunkt i strategien å tenke baklengs vil kunne:
- Legge til 2 og få 24 først. Regne videre: (24 : 3) ‧ 4 = 32. Bygger på med (32 : 4) ‧ 5 og får 40.
- Velge samme strategi som over, men med støtte i konkreter eller tegning.
- Bruke med utgangspunkt i det som er igjen til slutt:
Noen elever vil tenke at helheten er 24 før Lisa har tatt sine kaker, men vil deretter gjøre den feilen at de starter med å regne en firedel av det:
- (24 : 4) + 24= 30 → (30 : 5) + 30 = 36
- Som over, men ved bruk av konkreter eller tegning.
Noter gjerne på tavle under oppsummeringen mens gruppene presenterer sine løsningsforslag. Elevene beskriver og begrunner strategiene de har brukt. De som har arbeidet baklengs, bør kunne vise, forklare og argumentere for hvordan de fant antall kaker, og hvorfor de brukte motsatte regnearter.
Gode veiledningsspørsmål
Vær litt gnien med veiledningsspørsmålene. La elevene streve før du stiller dem.
- Hvordan vil dere løse oppgaven? Hva vil dere starte med? Hvorfor?
- Kan du lage en visuell representasjon (for eksempel en tegning) som kan hjelpe deg til å løse oppgaven?
- Har vi all den informasjonen vi trenger for å kunne løse oppgaven?
- Hvordan vil dere forklare framgangsmåten deres for de andre i klassen?
- Kan dere vise løsningen ved hjelp av andre representasjoner (tegninger/konkreter, tabeller, symboler).
- Hvilke regnearter bruker dere og hvorfor? Passer de til konteksten?
- Hvilke regnestykker beskriver situasjonen? Hva forteller regnestykkene? Hva har dere funnet ut?
Mulig støtte
Egnet konkretiseringsmateriell, for eksempel tellebrikker, kan være en god støtte for enkelte elever. Det er viktig at eleven klarer å se sammenhengen mellom den praktiske situasjonen med kakene og konkretene som skal brukes.
Dersom elevene har arbeidet lite med brøkbegrepet, kan det være lurt å arbeide med en lignende oppgave med færre barnebarn.
Elevsvar
På 5.trinn på Nyborg skole har elevene jobbet med oppgaven på vertikale taver, 3 og 3 elever i tilfeldig valgte grupper. Tavlene innbyr til å kunne skrive akkurat det man tenker der og da, og det er lett å viske bort det som er skrevet. Undervisningen inneholder også samtaler med elevene om hvilke strategier elevene bruker, og hva de tenker.
Gruppe 1 tok tak i informasjonen om at Nikolai og Mattias tar en brøkdel av kakene hver. Nikolai tok \(\frac15\) av kakene, og da må alle kakene være \(\frac55\). De har også funnet ut at før Lisa tok 2 kaker, og etter at Mattias tok \(\frac14\) av kakene, var det 24 kaker i boksen. De 24 kakene må utgjøre \(\frac34\). En av elevene ser at den \(\frac14\) Mattias tok var 8 kaker. Til høyre viser de en utregning på at det da stemmer at \(\frac15\) også er 8. I samtale med elevene strever de med å forklare hvordan de kom fram til dette, men de kan vise at det stemmer. Ut ifra dette kan de sette opp en oversikt over hvordan kakestjelingen har foregått, og at det må ha vært 40 kaker i boksen til å begynne med (i rød ramme).
Gruppe 2 bruker kunnskap de har lært fra før, og setter i gang med å finne et minste felles multiplum. Klassen har nylig holdt på med dette i undervisningen. De setter opp 5-gangen og 4-gangen og finner 40 som minste felles multiplum. Derfra kan de vise hvordan dette passer med kakestjelingen (i midten og oppe i hjørnet), og kan fortelle at 40 er det antallet kaker det må ha vært i boksen.
Send inn elevsvar
Ressursen er utviklet av Matematikksenteret