Småkaker i boksen
Aktivitet
Lisa, Nicolai og Mattias var på overnattingsbesøk hos bestefar og bestemor. Der var det ein boks med mange kaker. Barnebarna skulle få kaker dagen etter.
Då Lisa hadde lagt seg, klarte ikkje Nicolai å vente lenger. Han fann kakeboksen og tok \(\frac15\) av kakene. Før Mattias skulle leggje seg, tok han \(\frac14\) av kakene som då var i boksen. Vesle Lisa var tidleg oppe og tok 2 kaker. Då bestemor kom, såg ho at det var berre 22 kaker igjen.
Kor mange kaker hadde det vore i boksen?
Tilleggsspørsmål:
Bestemor hadde eigentleg tenkt at sidan Mattias var eldst, skulle han få \( {1\over 4}\) av alle kakene. Nicolai skulle få \( {1\over 5}\) av alle kakene, og vesle Lisa skulle få 2 kaker.
Tok dei tre barnebarna så mange småkaker som bestemor hadde planlagt at dei skulle få? Grunngi svaret!
Løysing
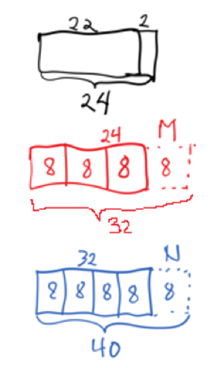
Vesle Lisa får 2 kaker. Før ho forsynte seg var det 24 kaker.
Dette er \( {3 \over 4}\) av dei kakene som var i boksen før Mattias forsynte seg med \( {1 \over 4}.\) Før Mattias forsynte seg, var det difor 32 kaker i boksen, og Mattias tok 8 kaker.
Dei 32 kakene er \( {4 \over 5}\) av dei kakene som var i boksen før Nicolai forsynte seg med sin del.
Det vil seie at det var 40 kaker i boksen før barnebarna kom på besøk, og Nicolai tok 8 kaker.
Lærarrettleiing
Kvifor arbeide med denne oppgåva?
Føremålet med aktiviteten er å arbeide med problemløysingsstrategiar. Oppgåva inviterer elevane til å ta i bruk strategien «tenkje baklengs». Elevane blir presenterte for eit problem der utgangspunktet er ukjent, og der det vil vere naturleg å tenkje baklengs. Dei fleste begynner med den informasjonen som er kjend, og som står i slutten av teksten. Elevane må analysere konteksten, reflektere over det som har skjedd undervegs, og kva rekningsart som beskriv hendinga. Kvar gong småkaker forsvinn frå kakeboksen, blir det beskrive ved hjelp av subtraksjon. Når elevane skal gå bakover i tid og beskrive den motsette hendinga, må dei bruke addisjon. Å forstå at rekningsarten blir motsett når dei arbeider baklengs, er avgjerande når ein bruker strategien «tenkje baklengs». Talet på kaker som borna tok (subtraksjon), må leggjast til når elevane arbeider baklengs (addisjon).
Det matematiske målet med aktiviteten er å utforske eigenskapar ved brøk som del av ein heil. Elevane må vite at brøkdelane av den same heile må vere like store. Dei får erfaring med at den heile kan variere, og at to ulike brøkar kan utgjere same mengde eller like mange når dei heile som dei skal reknast av, er forskjellige. Elevane er ofte flinke til å rekne brøkdelen av ein heil (mengde), men får problem når dei skal gå motsett veg og finne den heile.
Mogleg tilnærming
Du kan presentere oppgåva som ei forteljing for elevane. La elevane kome med forslag i plenum om korleis dei vil begynne arbeidet med problemet. Når dei skal begynne å arbeide, får dei utdelt oppgåva skriftleg, i tillegg til plastbrikker dei kan bruke om dei vil.
Denne oppgåva eignar seg fint som gruppeoppgåve og legg til rette for gode matematiske samtalar. Oppfordre gjerne gruppene til å uttrykkje løysingsforslaga sine både munnleg og skriftleg.
Elevane vil kunne løyse oppgåva på mange ulike måtar og med ulike strategiar. Dei vil kunne
- ta utgangspunkt i eit meir eller mindre tilfeldig tal, og sjekke om det blir 22 til slutt
- ta utgangspunkt i femgongen, fordi Nicolai skal ha ein femdel
Elevar som tek utgangspunkt i strategien «tenkje baklengs», vil kunne
- leggje til 2 og få 24 først, rekne vidare: (24 : 3) ‧ 4 = 32, byggje på med (32 : 4) ‧ 5 og få 40
- velgje same strategi som over, men med støtte i konkret eller teikning
- ta utgangspunkt i det som er igjen til slutt:
Somme elevar vil tenkje at den heile er 24 før Lisa har teke sine kaker, men vil deretter gjere den feilen at dei begynner med å rekne ein firedel av det:
- (24 : 4) + 24= 30 → (30 : 5) + 30 = 36
- som over, men ved bruk av konkret eller teikning
Noter gjerne på tavla under oppsummeringa medan gruppene presenterer løysingsforslaga sine. Elevane beskriv og grunngir strategiane dei har brukt. Dei som har arbeidd baklengs, bør kunne vise, forklare og argumentere for korleis dei fann talet på kaker, og kvifor dei brukte motsette rekningsartar.
Gode rettleiingsspørsmål
Ver litt gjerrig med rettleiingsspørsmåla. La elevane streve før du stiller dei.
- Korleis vil de løyse oppgåva? Kva vil de begynne med? Kvifor?
- Kan de lage ein visuell representasjon (f.eks. ei teikning) som kan hjelpe dykk til å løyse oppgåva?
- Har de all den informasjonen de treng for å kunne løyse oppgåva?
- Korleis vil de forklare framgangsmåten dykkar for dei andre i klassen?
- Kan de vise løysinga ved hjelp av andre representasjonar (teikningar/konkret, tabellar, symbol)?
- Kva rekningsartar bruker de, og kvifor? Passar dei til konteksten?
- Kva reknestykke beskriv situasjonen? Kva fortel reknestykka? Kva har de funne ut?
Mogleg støtte
Eigna konkretiseringsmateriell, for eksempel teljebrikker, kan vere ei god støtte for enkelte elevar. Det er viktig at elevane klarer å sjå samanhengen mellom den praktiske situasjonen med kakene og konkreta som skal brukast.
Dersom elevane har arbeidd lite med brøkomgrepet, kan det vere lurt å arbeide med ei liknande oppgåve med færre barnebarn.
Send inn elevsvar
Ressursen er utviklet av Matematikksenteret