Bretting av kvadratiske ark
Aktivitet
Bruk kvadratiske ark.
- Brett et kvadrat med nøyaktig \(\frac14\) av arkets areal.
- Brett en trekant med nøyaktig \(\frac14\) av arkets areal.
- Brett en annen trekant, som ikke er kongruent med den første trekanten, med nøyaktig \(\frac14\) av arkets areal.
- Brett et kvadrat som har halvparten av arkets areal.
- Brett et kvadrat til, som er orientert annerledes enn det første, med nøyaktig halvparten av arkets areal.
Oppgaven er laget med utgangspunkt i en ressurs fra boken Mathematical Mindsets av Jo Boaler.
Løsning
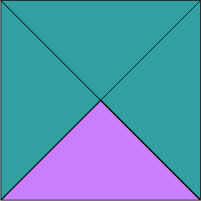
Figur 1:
Sidekanten til det røde kvadratet i figur 1 er en halv på grunn av brettingen.
Figur 2:
Bretting langs begge diagonalene gir fire like store trekanter. Denne oppgaven kan også løses ved hjelp av Pytagoras' setning. Katetene til den lilla trekanten i figur 2 er like lange som en halv diagonal.
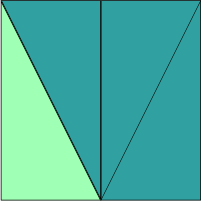
Figur 3:
Bretter man arket i to, dannes det to like rektangler. De blir delt langs diagonalen. Det betyr at den grønne trekanten i figur 3 har en katet som er lik lengden av arket, og en katet som er lik halve arket.
Figur 4:
Det turkisfargede kvadratet i figur 4 har areal \(\frac12\). Sammenlignet med figur 1 er det lik fire halve røde kvadrater.
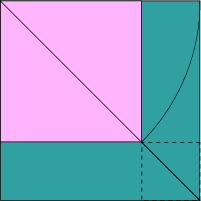
Figur 5:
Det rosa kvadratet i figur 5 har samme areal som det turkisfargede i figur 4, nemlig halvparten av arket. Diagonalen i det rosa kvadratet er lik siden av arket på grunn av brettingen.
Kaller vi siden i det store kvadratet a og siden i det rosa kvadratet x, blir \(a^2=2x^2\), og dermed blir \(x^2=\frac{a^2}{2}\)
Lærerveiledning
Hvorfor arbeide med denne oppgaven?
Denne oppgaven kan utvikle elevenes forståelse av areal i ulike geometriske figurer. Elevene oppfordres til å tenke kreativt for å argumentere for løsningene sine.
Med unntak av det siste spørsmålet er ikke brettingen utfordrende. Derimot vil en del elever ha vanskeligheter med å forklare med geometrisk resonnement hvorfor brettingen gir den ønskede figuren.
Mulig tilnærming
Introduser gjerne oppgaven muntlig samtidig som du viser den for elevene og deler ut kvadratiske ark. Åpne opp for spørsmål hvis noe er uklart for dem.
Elevene kan utforske problemene på egen hånd først, og de må argumentere for løsningene sine. Deretter kan de gå sammen i par, hvor de får hver sin rolle. En elev skal være overbeviser, og den andre skal være skeptiker. Skeptikeren skal stille kritiske spørsmål som kan få overbeviseren til å utbedre eller utdype argumentene sine, slik at forklaringen blir forståelig. Elevene bytter roller for hver oppgave.
Avslutt med en felles oppsummering. Velg en overbeviser og en skeptiker fra ulike par i oppsummeringen, og gjennomfør oppsummeringen på samme måte som pararbeidet. Vis løsninger på alle deloppgavene.
Gode veiledningsspørsmål
La elevene streve før du stiller veiledningsspørsmålene:
- Hvordan kan du dele arket i to? Finnes det flere måter å gjøre det på?
- Hvilke ulike linjer i kvadratet kan det være nyttig å bruke?
- Hvilke ulike linjer i trekanter kan det være nyttig å bruke?
- Hvordan kan man dele opp kvadrater?
- Hvordan vet du at den figuren du har brettet, er riktig?
Mulig utvidelse
Vis ved regning at de tre første arealene er like store, og at de to siste er like store.
Mulig støtte
Å diskutere egenskaper ved trekanter og firkanter, spesielt kvadrater, kan være nyttig for elever. Videre kan dere diskutere hvordan dere kan dele kvadrater i ulike trekanter.
Ressursen er utviklet av Matematikksenteret