Bretting av kvadratiske ark
Aktivitet
Bruk kvadratiske ark.
- Brett eit kvadrat med nøyaktig \(\frac14\) av arealet av arket.
- Brett ein trekant med nøyaktig \(\frac14\) av arealet av arket.
- Brett ein annan trekant, som ikkje er kongruent med den første trekanten, med nøyaktig \(\frac14\) av arealet av arket.
- Brett eit kvadrat som har halvparten av arealet av arket.
- Brett eit kvadrat til, som er orientert annleis enn det første, med nøyaktig halvparten av arealet av arket.
Oppgåva er laga med utgangspunkt i ein ressurs frå boka Mathematical Mindsets av Jo Boaler.
Løysing
Figur 1:
Sidekanten i det raude kvadratet på figur 1 er ein halv på grunn av brettinga.
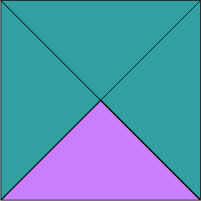
Figur 2:
Bretting langs begge diagonalane gir fire like store trekantar. Oppgåva kan også løysast ved hjelp av den pytagoreiske setninga. Katetane i den lilla trekanten på figur 2 er like lange som ein halv diagonal.
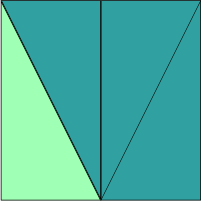
Figur 3:
Brettar vi arket i to, får vi to like rektangel. Dei blir delt langs diagonalen. Det betyr at den grøne trekanten på figur 3 har ein katet som er lik lengda av arket, og ein katet som er lik halve arket.
Figur 4:
Det turkisfarga kvadratet på figur 4 har areal \(\frac12\). Samanlikna med figur 1 er det lik fire halve raude kvadrat.
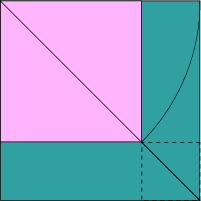
Figur 5:
Det rosa kvadratet i figur 5 har same areal som det turkisfarga i figur 4, nemleg halvparten av arket. Diagonalen i det rosa kvadratet er lik sida på arket på grunn av brettinga.
Kallar vi sida i det store kvadratet a og sida i det rosa kvadratet x, blir \(a^2=2x^2\), og dermed blir \(x^2=\frac{a^2}{2}\)
Lærarrettleiing
Kvifor arbeide med denne oppgåva?
Oppgåva kan gi elevane betre forståing av areal i ulike geometriske figurar. Elevane må tenkje kreativt for å argumentere for løysingane sine.
Med unntak av det siste spørsmålet er ikkje brettinga utfordrande. Derimot vil ein del elevar ha vanskar med å forklare med geometrisk resonnement kvifor brettinga gir den ynskte figuren.
Mogleg tilnærming
Introduser gjerne oppgåva munnleg samtidig som du viser henne for elevane og deler ut kvadratiske ark. Opne for spørsmål dersom noko er uklart for dei.
Elevane kan utforske problema på eiga hand først, og dei må argumentere for løysingane sine. Deretter kan dei gå saman i par, der dei får kvar si rolle. Ein elev skal vere overtydar, og den andre skal vere skeptikar. Skeptikaren skal stille kritiske spørsmål som kan få overtydaren til å betre eller utdjupe argumenta sine, slik at forklaringa blir forståeleg. Elevane byter roller for kvar oppgåve.
Avslutt med ei felles oppsummering. Vel ein overtydar og ein skeptikar frå ulike par i oppsummeringa, og gjennomfør oppsummeringa på same måten som pararbeidet. Vis løysingar på alle deloppgåvene.
Gode rettleiingsspørsmål
La elevane streve før du stiller rettleiingsspørsmåla:
- Korleis kan du dele arket i to? Finst det fleire måtar å gjere det på?
- Kva for ulike linjer i kvadrat kan det vere nyttig å bruke?
- Kva for ulike linjer i trekantar kan det vere nyttig å bruke?
- Korleis kan du dele opp kvadrat?
- Korleis veit du at den figuren du har bretta, er rett?
Mogleg utviding
Vis med rekning at dei tre første areala er like store, og at dei to siste er like store.
Mogleg støtte
Å diskutere eigenskapar ved trekantar og firkantar, særleg kvadrat, kan vere nyttig for elevane. De kan også diskutere korleis de kan dele kvadrat i ulike trekantar.
Ressursen er utviklet av Matematikksenteret