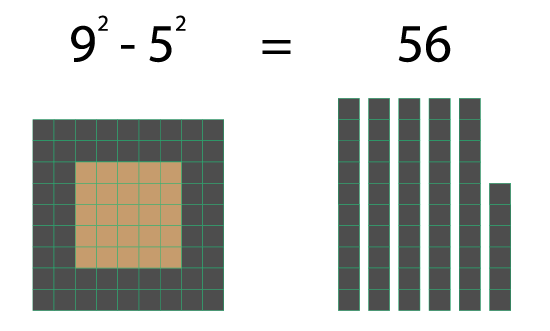
Hva er mulig?
Aktivitet
Mange tall kan skrives som differansen mellom to kvadrattall. For eksempel
\(\qquad 20=6^2-4^2\\ \qquad 21=5^2-2^2\\ \qquad 36=6^2-0^2\)
Hvor mange tall fra 1 til 30 kan dere skrive som differansen mellom to kvadrattall?
Noen spørsmål å tenke over:
- Hva legger dere merke til når dere studerer differansen mellom kvadratene til to påfølgende tall?
- Hva legger dere merke til hvis dere studerer differansene mellom kvadratene til to tall hvor det ene er 2 større enn det andre? Hva med tall som er 3 større enn det andre? Hva med 4?
- Når er differansen mellom to kvadrattall et oddetall?
- Og når er differansen et partall?
- Hva legger dere merke til med tall som ikke kan uttrykkes som differansen mellom to kvadrattall?
Kan dere bevise noe av det dere har funnet ut?
Starthjelp
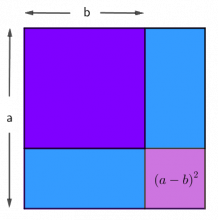
Dette bildet kan hjelpe dere med å bevise det dere har funnet ut.
Kall siden i det store kvadratet for a og i det mindre blå kvadratet for b.
- Hvilket område på figuren svarer til \(a^2-b^2?\)
- Hva slags tall kan være representert av et slikt område?
Løsning
OBS. Noen av disse tallene kan skrives som en differanse mellom to kvadrattall på flere måter.
\(\begin{array}{l} 1 = {1^2} - {0^2}\\ 2\:{\rm{ ingen\: løsning}}\\ 3 = {2^2} - {1^2}\\ 4 = {2^2} - {0^2}\\ 5 = {3^2} - {2^2}\\ 6\:{\rm{ ingen\: løsning}}\\ 7 = {4^2} - {3^2}\\ 8 = {3^2} - {1^2}\\ 9 = {5^2} - {4^2}\\ 10\:{\rm{ ingen\: løsning}}\\ 11 = {6^2} - {5^2}\\ 12 = {4^2} - {2^2}\\ 13 = {7^2} - {6^2}\\ 14\:{\rm{ ingen\: løsning}}\\ 15 = {8^2} - {7^2}\\ 16 = {5^2} - {3^2}\\ 17 = {9^2} - {8^2}\\ 18\:{\rm{ ingen \:løsning}}\\ 19 = {10^2} - {9^2}\\ 20 = {6^2} - {4^2}\\ 21 = {11^2} - {10^2}\\ 22\:{\rm{ ingen\: løsning}}\\ 23 = {12^2} - {11^2}\\ 24 = {7^2} - {5^2}\\ 25 = {13^2} - {12^2}\\ 26\:{\rm{ ingen\: løsning}}\\ 27 = {14^2} - {13^2}\\ 28 = {8^2} - {6^2}\\ 29 = {15^2} - {14^2}\\ 30\:{\rm{ ingen \:løsning}} \end{array}\)
Alle oddetall kan uttrykkes som differansen mellom kvadratene til to påfølgende tall:
\((n+1)^2-n^2=n^2+2n+1-n^2=2n+1.\) Dette gjelder for alle \(n\in \mathbb N\).
Hvis vi kvadrerer to tall med en differanse som er et oddetall og finner differansen mellom kvadratene, vil den være et oddetall. Med andre ord, - hvis vi kvadrerer et partall og et oddetall vil differansen alltid være et oddetall.
\(\begin{align}partall^2-oddetall^2&=(2k)^2-(2n-1)^2\\ &=4k^2-4n^2+4n-1\\ &=4(k^2-n^2+n)-1\\ &=partall-1\\ &=oddetall \end{align}\)
Men hvis vi kvadrerer to tall med en differanse som er et partall og finner differansen, vil den være et partall. Med andre ord, - hvis vi kvadrerer to partall eller to oddetall vil differansen alltid være et partall. Og det vil være et partall i 4-gangen!
\(\begin{align} {\rm{partal}}{{\rm{l}}^2} - {\rm{partal}}{{\rm{l}}^2} &= {(2n)^2} - {(2k)^2} \\ &= 4({n^2} - {k^2}) \\ &= {\rm{partall \:i\: 4 - gangen}}\\ \\ {\rm{oddetal}}{{\rm{l}}^2} - {\rm{oddetal}}{{\rm{l}}^2} &= {(2n - 1)^2} - {(2k - 1)^2} \\ &= 4{n^2} - 4n + 1 - 4{k^2} + 4k - 1\\ {\rm{ }} &= 4(n\, - n - {k^2} + k) \\ &= {\rm{partall\:i \:4 - gangen}} \end{align}\)
Partallene som ikke er i 4-gangen kan skrives på formen \(4n+2=2(2n+1)\).
Vi ser at de vil inneholde bare ett 2-tall og et oddetall når de faktoriseres. Oddetallet kan eventuelt faktoriseres i flere primtall, men de må alle være odde.
Påstanden er at tallene på formen \(4n+2=2(2n+1)\) ikke kan uttrykkes som en differanse mellom to kvadrattall.
Bevis:
La x være et partall som ikke er i 4-gangen, \(x=4n+2\).
Anta ta x kan skrives som en differanse mellom to kvadrattall, \(x=a^2-b^2=(a+b)(a-b)\).
La \(u=a+b\) og \(v=a-b\), slik at \(x=uv\). Da er differansen mellom de to faktorene:
\(u-v=(a+b)-(a-b)=2b\), altså et partall.
Men \(x=4n+2=2(2n+1)\). Faktorene i x vil alltid være ett partall og et eller flere oddetall, siden 2 er eneste partallsfaktor i tallet. Differansen mellom faktorene i x vil alltid bli et oddetall siden det er differansen mellom et partall og et oddetall.
Så kravet om at differansen mellom to faktorer i x skal være et partall vil aldri bli oppfylt. Dermed er det umulig at partallene som ikke er i 4-gangen kan uttrykkes som en differanse mellom to kvadrattall.
Konklusjon: Tall på formen \(4n+2\) kan ikke skrives som en differanse mellom to kvadrattall.
Visualisering av løsningen:
Differansen \(a^2-b^2\) er representert ved området som ikke er mørkeblått. Hvis vi lar siden i det store kvadratet være a og i det blå kvadratet være b, ser vi at differansen er \(2b(a-b)+(a-b)^2\).
\((a-b)^2\) er arealet av det lille kvadratet nederst i høyre hjørne.
De to rektanglene har til sammen areal \(2b(a-b)\), dette er alltid et partall.
Hvis arealet av det lille kvadratet i nederst til høyre er et oddetall (1, 9, 25, ..osv), blir differansen:
\(\begin{align}a^2-b^2&=2b(a-b)+(a-b)^2\\ &=partall+oddetall\\ &=oddetall \end{align}\)
Vi kan velge \(a-b=1.\) Da kan vi uttrykke alle oddetall som en differanse mellom kvadratet av to påfølgende heltall.
Hvis arealet av kvadratet nede til høyre er et partall (4, 16, 36, ..), ser vi at dette alltid blir tall i 4-gangen. I disse tilfellene er alltid \(a-b\) et partall, så både \(2b(a-b)\) og \((a-b)^2\) blir tall i 4-gangen. Da blir også \(a^2-b^2=2b(a-b)+(a-b)^2\) et tall i 4-gangen. Så vi kan uttrykke alle tall i 4-gangen som en differanse mellom to kvadrattall.
Differansen \(a^2-b^2=2b(a-b)+(a-b)^2\) kan aldri bli et partall som ikke er i 4-gangen, for da måtte summen av arealene av de to rektanglene vært et partall som ikke var i 4-gangen. Men hvis \(a-b\) er et partall blir både summen av arealene av de to rektanglene og arealet av kvadratet nederst til høyre tall i 4-gangen.
Lærerveiledning
Hvorfor arbeide med denne oppgaven?
Denne oppgaven starter med å be elevene prøve å uttrykke alle tall som en differanse mellom to kvadrattall, og den foreslår noen mulige måter å undersøke dette på. Dette kan brukes som et springbrett for generalisering og for å bruke algebra for å beskrive og bevise. Under arbeidet får elevene anledning til å bruke den viktige likheten \(a^2-b^2=(a+b)(a-b)\).
Du kan finne oppgaven på en kopieringsoriginal her.
Mulig tilnærming
Arbeidet kan starte med at læreren ber elevene nevne et tosifret tall under 30. Skriv det på tavla og skriv det som en differanse mellom to kvadrattall. Gjenta dette noen ganger.
Utfordre så elevene til å prøve å skrive alle tall mellom 1 og 30 som differanser mellom to kvadrattall. Be dem skrive flere enn en løsning der det er mulig.
Når de fleste har løst oppgavene kan de dele løsningene i hele klassen. Skriv alle løsningene på tavla.
«Se på løsningen så langt. Hva legger dere merke til?»
Gi elevene litt tid til å diskutere før dere tar en ny fellessamtale. Her er noen påstander, observasjoner og spørsmål elevene kan komme med:
- Differansen mellom to kvadrattall blir alltid et oddetall.
- Differansen mellom kvadrater av påfølgende tall er lik summen av de to påfølgende tallene.
- Hva skjer hvis jeg finner differansen mellom to tall der det ene er 2 større enn det andre?
- Tall som kan skrives på mer enn en måte har mange faktorer.
- Når er differansen mellom to kvadrattall et oddetall.
- Og når er den et partall?
- Hvorfor er det noen tall som ser ut til å ikke kunne uttrykkes som en differanse mellom to kvadrattall?
- Kan vi forutsi hvilke tall som ikke kan skrives som en differanse mellom to kvadrattall?
Alternativt kan læreren introdusere problemet på denne måten:
La klassen arbeide i grupper på to eller tre elever og gi hver gruppe dette arket. På arket er uttrykkene ordnet i grupper på tre og tre, der hver gruppe består uttrykk som har noe til felles. Be elevene diskutere hva som kan være felles for uttrykkene som er satt opp sammen, og om de kan finne flere uttrykk som hører til i samme gruppene. Hvilke påstander og hvilke spørsmål kan man stille etter å ha studert disse uttrykkene?
La så hele klassen samles for å dele det de har funnet ut. Hvilke påstander vil de komme med og hvilke spørsmål vil de stille til det de har oppdaget? Vil noen få svar på spørsmålene sine så snart de får se og høre andre gruppers forklaringer? Sørg for at det elevene har funnet ut og de spørsmålene de har stilt, blir notert på tavla.
En måte å få elevene i gang med å undersøke mønstrene som ligger i uttrykkene som er satt sammen på oppgavearkene, kan være å be dem finne tall mellom 1 og 30 og uttrykke dem som differanser mellom kvadrattall, - på flere måter hvis det er mulig. Oppmuntre dem til å undersøke systematisk og lage notater som gjør det oversiktlig og mulig å se mønstre og sammenhenger. Når de har funnet en del løsninger, kan de dele det de har funnet i fellesskap. Noter løsninger, påstander og spørsmål på tavla.
Oppmuntre elevene til å stille spørsmål og undersøke, og til å prøve å finne forklaringer, begrunnelser og kanskje bevis for sammenhenger som ser ut til å gjelde.
La elevene stå fritt til å velge algebraiske eller visuelle representasjoner.
Avslutt i plenum der elevene presenterer det de har funnet ut. Forvent at de er tydelige og presise. Oppmuntre elevene til å utfordre hverandre hvis noe i et bevis eller en forklaring er uklart, og få dem til å foreslå måter å gjøre det klarere på.
Avslutningen av økta kan være: «Nå kommer jeg til å gi dere noen tall og be dere om raskt å finne en eller flere måter å uttrykke dette tallet som en differanse mellom kvadrattall, eller å overbevise meg om at det er mulig eller ikke.»
Gode veiledningsspørsmål
- Hva legger dere merke til når dere studerer differansen mellom kvadratene til to påfølgende tall? Hva hvis dere studerer differansene mellom kvadratene til to tall hvor det ene er 2, 3, 4, … større enn det andre?
- Når er differansen mellom to kvadrattall et oddetall?
- Og når er differansen et partall?
- Hva legger dere merke til med tall som ikke kan uttrykkes som differansen mellom to kvadrattall?
- Kan dere bevise noe av det dere har funnet ut?
Mulig utvidelser av oppgaven
- Alle odde primtall kan skrives som differansen mellom to kvadrattall. Vis at et odde primtall kan skrives som en differanse mellom to kvadrattall på bare én måte, og at dette er differansen mellom to påfølgende kvadrattall.
- 120 kan skrives som en differanse mellom to kvadrattall på følgende måter:
\(31^2-29^2\\ 17^2-13^2\\ 13^2-7^2\\ 11^2-1^2\)
Finn alle mulige måter å skrive 924 på som en differanse mellom to kvadrattall. Kan du bevise at du har funnet alle mulige?
Virkelig utfordrende:
Finn en måte for å finne ut hvor mange måter ethvert tall kan skrives på som en differanse mellom to kvadrattall.
Mulig støtte
Elevene kan få hjelp til å systematisere det de finner, for eksempel ved å lage en tabell der det er en kolonne for tall med differanse 1, en kolonne for tall med differanse 2 osv.
| Tall | Differanse mellom kvadrater av to påfølgende tall | Differanse mellom kvadrater av to tall med differanse 2 | Differanse mellom kvadrater av to tall med differanse 3 | osv... |
| 1 | \(1^2-0^2\) | |||
|---|---|---|---|---|
| 2 | ||||
| 3 | \(2^2-1^2\) | |||
| 4 | \(2^2-0^2\) | |||
| 5 | \(3^2-2^2\) | |||
| 6 | ||||
| 7 | \(4^2-3^2\) | |||
| 8 | \(3^2-1^2\) | |||
| 9 | \(5^2-4^2\) | \(3^2-0^2\) |
Ressursen er utviklet av NRICH