Kva er mogleg?
Aktivitet
Mange tal kan skrivast som differansen mellom to kvadrattal. Nokre eksempel:
\(\qquad 20=6^2-4^2\\ \qquad 21=5^2-2^2\\ \qquad 36=6^2-0^2\)
Kor mange tal frå 1 til 30 kan de skrive som differansen mellom to kvadrattal?
Nokre spørsmål å tenkje over:
- Kva legg de merke til når de studerer differansen mellom kvadrata av to etterfølgjande tal?
- Kva legg de merke til dersom de studerer differansane mellom kvadrata av to tal der det eine er 2 større enn det andre? Korleis blir det med tal som er 3 større enn det andre? 4 større enn det andre?
- Når er differansen mellom to kvadrattal eit oddetal?
- Og når er differansen mellom to kvadrattal eit partal?
- Kva legg de merke til med tal som ikkje kan uttrykkjast som differansen mellom to kvadrattal?
Kan de bevise noko av det de har funne ut?
Starthjelp
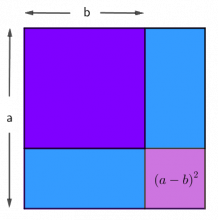
Figuren ovanfor kan hjelpe dykk med å bevise det de har funne ut.
Kall sida i det store kvadratet a og sida i det mindre, blå kvadratet b.
- Kva for eit område på figuren svarar til \(a^2-b^2?\)
- Kva slags tal kan vere representerte av eit slikt område?
Løysing
OBS! Nokre av desse tala kan skrivast som ein differanse mellom to kvadrattal på fleire måtar.
\(\begin{array}{l} 1 = {1^2} - {0^2}\\ 2\:{\rm{ inga\: løysing}}\\ 3 = {2^2} - {1^2}\\ 4 = {2^2} - {0^2}\\ 5 = {3^2} - {2^2}\\ 6\:{\rm{ inga\: løysing}}\\ 7 = {4^2} - {3^2}\\ 8 = {3^2} - {1^2}\\ 9 = {5^2} - {4^2}\\ 10\:{\rm{ inga\: løysing}}\\ 11 = {6^2} - {5^2}\\ 12 = {4^2} - {2^2}\\ 13 = {7^2} - {6^2}\\ 14\:{\rm{ inga\: løysing}}\\ 15 = {8^2} - {7^2}\\ 16 = {5^2} - {3^2}\\ 17 = {9^2} - {8^2}\\ 18\:{\rm{ inga\: løysing}}\\ 19 = {10^2} - {9^2}\\ 20 = {6^2} - {4^2}\\ 21 = {11^2} - {10^2}\\ 22\:{\rm{ inga\: løysing}}\\ 23 = {12^2} - {11^2}\\ 24 = {7^2} - {5^2}\\ 25 = {13^2} - {12^2}\\ 26\:{\rm{ inga\: løysing}}\\ 27 = {14^2} - {13^2}\\ 28 = {8^2} - {6^2}\\ 29 = {15^2} - {14^2}\\ 30\:{\rm{ inga \:løysing}} \end{array}\)
Alle oddetal kan uttrykkjast som differansen mellom kvadrata av to etterfølgjande tal:
\((n+1)^2-n^2=n^2+2n+1-n^2=2n+1.\) Dette gjeld for alle \(n\in \mathbb N\).
Dersom vi kvadrerer to tal med ein differanse som er eit oddetal, og finn differansen mellom kvadrata, vil han vere eit oddetal. Med andre ord: Dersom vi kvadrerer eit partal og eit oddetal, vil differansen alltid vere eit oddetal.
\(\begin{align}partal^2-oddetal^2&=(2k)^2-(2n-1)^2\\ &=4k^2-4n^2+4n-1\\ &=4(k^2-n^2+n)-1\\ &=partal-1\\ &=oddetal \end{align}\)
Men dersom vi kvadrerer to tal med ein differanse som er eit partal, og finn differansen, vil han vere eit partal. Med andre ord: Dersom vi kvadrerer to partal eller to oddetal, vil differansen alltid vere eit partal. Og det vil vere eit partal i 4-gongen!
\(\begin{align} {\rm{parta}}{{\rm{l}}^2} - {\rm{parta}}{{\rm{l}}^2} &= {(2n)^2} - {(2k)^2} \\ &= 4({n^2} - {k^2}) \\ &= {\rm{partal \:i\: 4 - gongen}}\\ \\ {\rm{oddeta}}{{\rm{l}}^2} - {\rm{oddeta}}{{\rm{l}}^2} &= {(2n - 1)^2} - {(2k - 1)^2} \\ &= 4{n^2} - 4n + 1 - 4{k^2} + 4k - 1\\ {\rm{ }} &= 4(n\, - n - {k^2} + k) \\ &= {\rm{partal\:i \:4 - gongen}} \end{align}\)
Partala som ikkje er i 4-gongen kan skrivast på forma \(4n+2=2(2n+1)\).
Vi ser at dei vil innehalde berre eitt 2-tal og eitt oddetal når dei blir faktoriserte. Oddetalet kan eventuelt faktoriserast i fleire primtal, men dei må alle vere odde.
Påstanden er at tala på forma \(4n+2=2(2n+1)\) ikkje kan uttrykkjast som ein differanse mellom to kvadrattal.
Bevis:
La x vere eit partal som ikkje er i 4-gongen, \(x=4n+2\).
Set at x kan skrivast som ein differanse mellomto kvadrattal, \(x=a^2-b^2=(a+b)(a-b)\).
La \(u=a+b\) og \(v=a-b\), slik at \(x=uv\). Då er differansen mellom dei to faktorane
\(u-v=(a+b)-(a-b)=2b\), altså eit partal.
Men \(x=4n+2=2(2n+1)\). Faktorane i x vil alltid vere eitt partal og eitt eller fleire oddetal, sidan 2 er den einaste partalsfaktoren i talet. Differansen mellom faktorane i x vil alltid bli eit oddetal, sidan det er differansen mellom eit partal og eit oddetal.
Kravet om at differansen mellom to faktorar i x skal vere eit partal, vil altså aldri bli oppfylt. Dermed er det umogleg at partala som ikkje er i 4-gongen, kan uttrykkjast som ein differanse mellom to kvadrattal.
Konklusjon: Tal på forma \(4n+2\) kan ikkje skrives som ein differanse mellom to kvadrattal.
Visualisering av løysinga:
Differansen \(a^2-b^2\) er representert ved området som ikkje er mørkeblått. Dersom vi let sida i det store kvadratet vere a og sida i det blå kvadratet vere b, ser vi at differansen er \(2b(a-b)+(a-b)^2\).
\((a-b)^2\) er arealet av det vesle kvadratet nederst i høgre hjørne.
Dei to rektangla har til saman arealet \(2b(a-b)\), og det er alltid eit partal.
Dersom arealet av det vesle kvadratet nedst til høgre er eit oddetal (1, 9, 25, ..osv), blir differansen:
\(\begin{align}a^2-b^2&=2b(a-b)+(a-b)^2\\ &=partal+oddetal\\ &=oddetal \end{align}\)
Vi kan velje \(a-b=1.\) Då kan vi uttrykkje alle oddetal som ein differanse mellom kvadratet av to etterfølgjande heiltal.
Dersom arealet av kvadratet nedst til høgre er eit partal (4, 16, 36, ..), ser vi at dette alltid blir tal i 4-gongen. I desse tilfella er \(a-b\) alltid eit partal, så både \(2b(a-b)\) og \((a-b)^2\) blir tall i 4-gangen. Då blir også \(a^2-b^2=2b(a-b)+(a-b)^2\) eit tal i 4-gongen. Så vi kan uttrykkje alle tal i 4-gongen som ein differanse mellom to kvadrattal.
Differansen \(a^2-b^2=2b(a-b)+(a-b)^2\) kan aldri bli eit partal som ikkje er i 4-gongen, for då måtte summen av areala av dei to rektangla vore eit partal som ikkje var i 4-gongen. Men dersom \(a-b\) er eit partal, blir både summen av areala av dei to rektangla og arealet av kvadratet nedst til høgre tal i 4-gongen.
Lærarrettleiing
Kvifor arbeide med denne oppgåva?
Oppgåva begynner med at elevane skal prøve å uttrykkje alle tal som ein differanse mellom to kvadrattal, og føreslår nokre moglege måtar å undersøkje det på. Dette kan brukast som eit springbrett for generalisering og for å bruke algebra til å beskrive og bevise. Under arbeidet får elevane høve til å bruke den viktige likskapen \(a^2-b^2=(a+b)(a-b)\).
Du kan finne oppgåva på ein kopieringsoriginal her (bokmål).
Mogleg tilnærming
Arbeidet kan begynne med at læraren ber elevane nemne eit tosifra tal under 30. Skriv det på tavla som ein differanse mellom to kvadrattal. Gjenta dette nokre gonger.
Utfordre så elevane til å skrive alle tal mellom 1 og 30 som differansar mellom to kvadrattal. Be dei skrive fleire enn éi løysing der det er mogleg.
Når dei fleste har løyst oppgåvene, kan dei dele løysingane i heile klassen. Skriv alle løysingane på tavla.
«Sjå på løysinga de har funne til no. Kva legg de merke til?»
Gi elevane litt tid til å diskutere før de tek ein ny fellessamtale. Her er nokre påstandar, observasjonar og spørsmål som elevane kan kome med:
- Differansen mellom to kvadrattal blir alltid eit oddetal.
- Differansen mellom kvadrat av etterfølgjande tal er lik summen av dei to etterfølgjande tala.
- Kva skjer dersom eg finn differansen mellom to tal der det eine er 2 større enn det andre?
- Tal som kan skrivast på meir enn éin måte, har mange faktorar.
- Når er differansen mellom to kvadrattal eit oddetal?
- Og når er differansen mellom to kvadrattal eit partal?
- Kvifor er det nokre tal som vi ikkje kan uttrykkje som ein differanse mellom to kvadrattal?
- Kan vi føreseie kva tal som ikkje kan skrivast som ein differanse mellom to kvadrattal?
Alternativt kan læraren introdusere problemet på denne måten:
La klassen arbeide i grupper på to eller tre elevar, og gi kvar gruppe dette arket. På arket er uttrykka ordna i grupper på tre og tre, og kvar gruppe inneheld uttrykk som har noko til felles. Be elevane diskutere kva som kan vere felles for uttrykka som er sette opp saman, og sjå om dei kan finne fleire uttrykk som høyrer til i dei same gruppene. Kva for påstandar og spørsmål kan dei stille etter å ha studert desse uttrykka?
La så heile klassen samlast for å dele det dei har funne ut. Kva for påstandar vil dei kome med, og kva for spørsmål vil dei stille til det dei har oppdaga? Vil somme få svar på spørsmåla sine så snart dei får sjå og høyre forklaringane til andre grupper? Sørg for at det elevane har funne ut, og dei spørsmåla dei har stilt, blir noterte på tavla.
Ein måte å få elevane i gang med å undersøkje mønstra som ligg i uttrykka som er sette saman på oppgåvearka, kan vere å be dei finne tal mellom 1 og 30 og uttrykkje dei som differansar mellom kvadrattal – på fleire måtar dersom det er råd. Oppmuntre dei til å undersøkje systematisk og lage notat som gjer det oversiktleg og mogleg å sjå mønster og samanhengar. Når dei har funne ein del løysingar, kan dei i fellesskap dele det dei har funne. Noter løysingar, påstandar og spørsmål på tavla.
Oppmuntre elevane til å stille spørsmål og undersøkje, og til å prøve å finne forklaringar, grunngivingar og kanskje bevis for samanhengar som ser ut til å gjelde.
La elevane stå fritt til å velje algebraiske eller visuelle representasjonar.
Avslutt i plenum der elevane presenterer det dei har funne ut. Dei må vere tydelege og presise. Oppmuntre elevane til å utfordre kvarandre dersom noko i eit bevis eller ei forklaring er uklart, og få dei til å føreslå måtar å gjere det klarare på.
Avslutninga av økta kan vere slik: «No kjem eg til å gi dykk nokre tal og be dykk om raskt å finne ein eller fleire måtar å uttrykkje desse tala på som ein differanse mellom kvadrattal, eller å overtyde meg om at det er mogleg eller ikkje mogleg.»
Gode Rettleiingsspørsmål
- Kva legg de merke til når de studerer differansen mellom kvadrata av to etterfølgjande tal?
- Kva legg de merke til dersom de studerer differansane mellom kvadrata av to tal der det eine er 2, 3, 4, … større enn det andre
- Når er differansen mellom to kvadrattal eit oddetal?
- Når er differansen mellom to kvadrattal eit partal?
- Kva legg de merke til med tal som ikkje kan uttrykkjast som differansen mellom to kvadrattal?
- Kan de bevise noko av det de har funne ut?
Mogleg utviding
- Alle odde primtall kan skrivast som differansen mellom to kvadrattal. Vis at eit odde primtal kan skrivast som ein differanse mellom to kvadrattal på berre éin måte, og at det er differansen mellom to etterfølgjande kvadrattal.
- 120 kan skrivast som ein differanse mellom to kvadrattal på desse måtane:
\(31^2-29^2\\ 17^2-13^2\\ 13^2-7^2\\ 11^2-1^2\) - Finn alle moglege måtar å skrive 924 på som ein differanse mellom to kvadrattal. Kan du bevise at du har funne alle moglege måtar?
Verkeleg utfordrande:
Finn ut kor mange måtar du kan skrive kva som helst tal på som ein differanse mellom to kvadrattal.
Mogleg støtte
Elevane kan få hjelp til å systematisere det dei finn, for eksempel ved å lage ein tabell der det er ein kolonne for tal med differanse 1, ein kolonne for tal med differanse 2, osv.
| Tall | Differanse mellom kvadratet av to etterfølgjande tal | Differanse mellom kvadratet av to tal med differanse 2 | Differanse mellom kvadratet av to tal med differanse 3 | osv... |
| 1 | \(1^2-0^2\) | |||
|---|---|---|---|---|
| 2 | ||||
| 3 | \(2^2-1^2\) | |||
| 4 | \(2^2-0^2\) | |||
| 5 | \(3^2-2^2\) | |||
| 6 | ||||
| 7 | \(4^2-3^2\) | |||
| 8 | \(3^2-1^2\) | |||
| 9 | \(5^2-4^2\) | \(3^2-0^2\) |
Ressursen er utviklet av NRICH