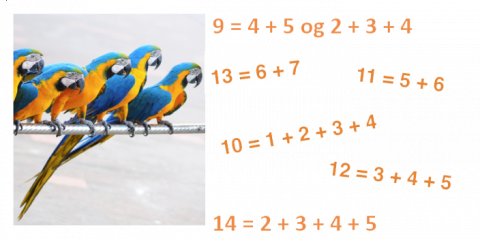Summer av påfølgende tall
Aktivitet
Noen tall er lik summen av påfølgende tallPåfølgende tall er tall som følger hverandre i rekkefølge fra minste til største, i vanlig tellerekkefølge..
- Kan du skrive alle tall på denne måten?
- Hvilke tall kan skrives på mer enn én måte?
Jonas har tenkt på summer av påfølgende tall. Her er noe av det han noterte:
Amalie kikket over skulderen hans og så på notatene:
- «Jeg lurer på om vi kan skrive alle tall som en sum av påfølgende tall.»
- «Noen tall kan skrives på mer enn én måte. Jeg lurer på hvilke tall det er.»
- «9, 12 og 15 kan alle skrives som en sum av tre påfølgende tall. Jeg lurer på om alle tall i 3-gangen kan skrives på denne måten.»
- «Kanskje man da kan skrive alle tall i 4-gangen som en sum av fire påfølgende tall …»
Prøv å finne svar på noen av spørsmålene til Amalie, eller still dine egne spørsmål, og prøv å finne svar på dem.
Kan du trekke noen konklusjoner?
Kan du gi overbevisende argumenter eller bevis for konklusjonene du har kommet fram til?
Starthjelp
- Begynn med å legge sammen noen påfølgende tall. Du kan for eksempel undersøke hvilke tall du får når du legger sammen to eller tre påfølgende tall.
- Sammenlign disse to summene med tre påfølgende tall:
1 + 2 + 3 = 6
2 + 3 + 4 = 9
Kan du forklare hvorfor summen her økte med 3?
Løsning
- Her er det ingen enkel løsning, men mange ulike forhold å oppdage.
Hvis vi legger sammen to påfølgende tall, får vi alltid et oddetall.
1 + 2 = 3
2 + 3 = 5
3 + 4 = 7
4 + 5 = 9
osv.
Summen øker med 2 for hver gang.
- Hvis vi legger sammen tre påfølgende tall, blir summen alltid et tall i 3-gangen.
1 + 2 + 3 = 6
2 + 3 + 4 = 9
3 + 4 + 5 = 12
4 + 5 + 6 = 15
5 + 6 + 7 = 18
osv.
Summen øker med 3 for hver gang.
- Hvis vi legger sammen et odde antall påfølgende tall, blir summen alltid det midterste tallet (gjennomsnittet av tallene) multiplisert med antall tall vi legger sammen. Hvorfor?
- Hvis vi legger sammen fire påfølgende tall, blir summen alltid et partall som er det dobbelte av et oddetall. Hvorfor?
1 + 2 + 3 + 4 = 10
2 + 3 + 4 + 5 = 14
3 + 4 + 5 + 6 = 18
osv.
Her øker summen med 4 for hver gang.
- Ikke alle tall kan skrives som en sum av påfølgende tall, det gjelder for eksempel 2, 4 og 8.
Det viser seg at dette vil gjelde for alle potenser av 2 (\(2^n\)).
2
3 = 1 + 2
4
5 = 2 + 3
6 = 1 + 2 + 3
7 = 3 + 4
8
9 = 4 + 5 = 2 + 3 + 4
10 = 1 + 2 + 3 + 4
11 = 5 + 6
12 = 3 + 4 + 5
13 = 6 + 7
14 = 2 + 3 + 4 + 5
15 = 7 + 8 = 4 + 5 +6 = 1 + 2 + 3 + 4 + 5
Bevis:
- Hvis vi legger sammen et odde antall påfølgende tall, blir summen lik det midterste tallet (gjennomsnittet av tallet) multiplisert med antall tall i summen.
Dvs. \(sum=gjennomsnitt\cdot antall\:påfølgende \:tall=et \:helt \:tall \cdot et \:oddetall\)
\(2^n\) kan ikke ha et oddetall som faktor, så et produkt av et oddetalls påfølgende faktorer kan aldri bli et tall på formen \(2^n\).
- Hvis vi legger sammen et partalls antall påfølgende tall, vil gjennomsnittet (summen av alle tallene delt på antall tall i summen) = summen av de to midterste tallene delt på to.
\(\begin{align}sum&=(sum\:av\:de\:to\:midterste\:tallene\cdot\frac12\cdot antall\:påfølgende\:tall)\\ &=(sum\:av\:to\:påfølgende\:tall)\cdot\left(\frac12\cdot partall\right)\\ &=(sum\:av\:to\:påfølgende\:tall)\cdot heltall\\ &=oddetall\cdot heltall \end{align} \)
Siden en av faktorene er et oddetall, kan heller ikke denne summen være et tall på formen \(2^n\)
Konklusjon: Summer av påfølgende tall kan aldri bli et tall på formen \(2^n\).
Lærerveiledning
Vær oppmerksom på at oppgaven er gitt skriftlig i to versjoner. Dere kan bruke kopieringsoriginalen som finnes her. Eller bruk fortellingen om Jonas og Amalie og spørsmålene knyttet til den.
Hvorfor arbeide med denne oppgaven?
Denne oppgaven er en enkel kontekst som gir elevene mulighet til å begynne å utforske egenskaper som tallene har. De kan se sammenhenger og kanskje utvikle noen sofistikerte algebraiske argumenter og bevis.
Mulig tilnærming
Du kan begynne med å vise videoen som du finner her.Samme lenke som ovenfor Eller du kan vise den underveis der det passer i introduksjonen.
For å introdusere problemet kan du begynne med å spørre: «Kan noen foreslå mengder på to eller flere påfølgende tall?» Skriv noen få forslag på tavla.
«Hva får vi hvis vi legger sammen de påfølgende tallene i hver av mengdene?» Skriv + mellom tallene, la elevene regne og skrive svarene.
«Alle disse svarene er eksempler på tall som kan skrives som summen av påfølgende tall. Tror dere alle tall kan skrives på en slik måte?»
«Kan vi prøve å skrive alle tallene fra 1 til 30 som summer av påfølgende tall?»
La elevene arbeide sammen i par mens du skriver tallene fra 1 til 30 på tavla, og gjør klar til å skrive inn elevenes løsninger.
Hvis noen spør om de får lov til å bruke negative tall, kan du for eksempel svare: «Hold dere til positive tall nå, så kan vi kanskje forske på negative tall senere.»
Så snart de fleste har funnet mange løsninger, kan de samles på tavla.
«Se på disse svarene, og forbered dere på å snakke om interessante ting dere oppdager.»
La elevene få tid til å tenke alene først, og deretter diskutere med en partner før diskusjonen i hele klassen.
Samle alle innspill og skriv dem på tavla som spørsmål eller påstander. Hvis ingen elever har noen ideer eller påstander, kan dere bruke spørsmålene som Amalie stiller.
La elevparene velge spørsmål de vil prøve å finne ut av. Si at de må forberede seg på å gi overbevisende argumenter for å forklare det de har kommet fram til.
Hvis det passer for klassen, kan dere i fellesskap se på hvordan man kan representere påfølgende tall algebraisk (n, n + 1, n + 2 …), slik at elevene får verktøy til algebraiske bevis.
Denne oppgaven inneholder mange problemstillinger og løsninger. Sørg for at de problemene elevene har valgt og arbeidet med, blir presentert og diskutert, og at det blir klart hva som er riktige løsninger på dem.
Gode veiledningsspørsmål
- Hva skjer når du legger sammen to påfølgende tall? Hva om du legger sammen tre påfølgende tall? Fire påfølgende tall?
- Hva merker du deg ved tall som ikke kan skrives som en sum av påfølgende tall?
- Hvis det første tallet i en mengde av påfølgende tall er n, hvordan kan du skrive algebraisk de følgende tallene i mengden, og dermed summen av tallene?
Mulig utvidelse
Utfordre elevene til å finne ut på hvor mange ulike måter ethvert tall x kan skrives som en sum av påfølgende tall.
En mer krevende utfordring:
Vis at det ikke er mulig å skrive \(2^n\) som en sum avpåfølgende tall, uansett hvilken verdi av n vi velger.
Mulig støtte
Klassens løsninger for tallene fra 1 til 30 kan de samles i en tabell som gir oversikt over ulike antall ledd i summen:
| 9 = | 4 + 5 | 2 + 3 + 4 | ||
| 10 = | 1 + 2 + 3 + 4 | |||
| 11 = | 5 + 6 | |||
| 12 = | 3 + 4 + 5 | |||
| 13 = | 6 + 7 | |||
| 14 = | 2 + 3 + 4 + 5 | |||
| 15 = | 7 + 8 | 4 + 5 + 6 | 1 + 2 + 3 + 4 + 5 |
Send inn elevsvar
Ressursen er utviklet av NRICH