Skiftende areal, skiftende omkrets
Aktivitet
Her er ni figurer. Du kan skrive dem ut fra kopioriginalen i menyen.
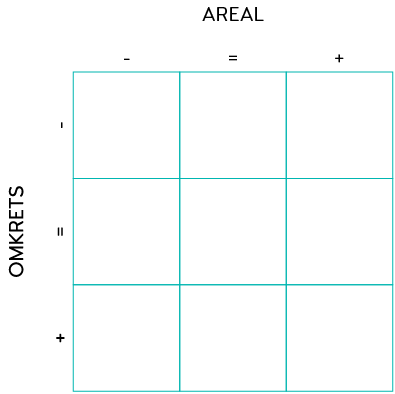
Utfordringen er å plassere figurene i rutenettet under.
Når du går fra venstre til høyre, øker arealet av figuren.
Når du går fra toppen til bunnen, øker omkretsen til figuren.
Alle figurene i den midterste kolonnen har samme areal.
Alle figurene i den midterste raden har samme omkrets.
Hvordan kan du resonnere for å avgjøre hvor hver figur skal plasseres?
Her er dimensjonene til ni rektangler. Disse kan skrives ut fra kopioriginalen i menyen til venstre.
| 2⋅8 | 4⋅4 | 1⋅15 |
| 5⋅5 | 3⋅8 | 2⋅7 |
| 1⋅16 | 3⋅6 | 1⋅9 |
Kan du plassere disse rektanglene i et rutenett på samme måte?
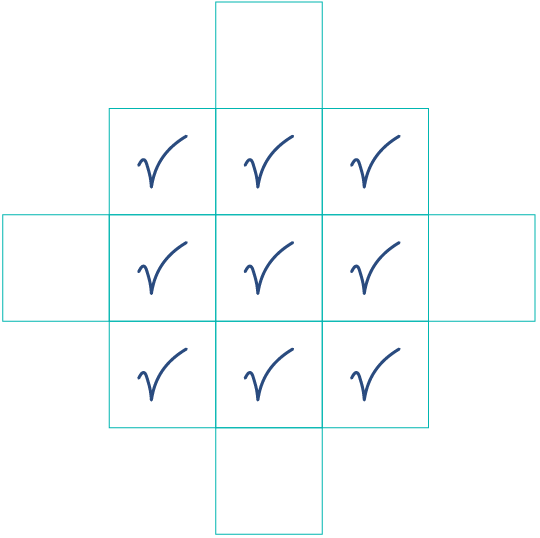
Når du har plassert de ni kortene, kan du se på rutenettet under.
Hakene representerer de ni kortene du allerede har plassert.
Kan du lage kort med dimensjoner for rektangler som kan plasseres i de fire tomme rutene, og som oppfyller de samme kriteriene?
Det er ikke mulig å fylle alle rutene. Kan du forklare hvorfor?
Kan du lage et sett med kort som kan plasseres på samme måte, hvis kortet i midten er et rektangel med dimensjoner 1 · 5?
Starthjelp
Hvis du synes det er vanskelig å forstå rutenettet, kan du ta en titt på dette bildet.
Robotene er plassert ut fra bredde og høyde, på samme måte som kortene skal plasseres etter areal og omkrets:
Når du går fra venstre til høyre, øker bredden på roboten.
Når du går fra toppen til bunnen, øker høyden på roboten.
Alle robotene i den midterste kolonnen har samme bredde.
Alle robotene i den midterste raden har samme høyde.
Lærerveiledning
Hvorfor arbeide med denne oppgaven?
Når elevene arbeider med denne oppgaven, kan de få dypere forståelse av areal og omkrets, og hvordan disse størrelsene endrer seg når formen på figuren endres. Aktiviteten tar for seg den misoppfatningen at når arealet øker, må også omkretsen øke.
Mulig tilnærming
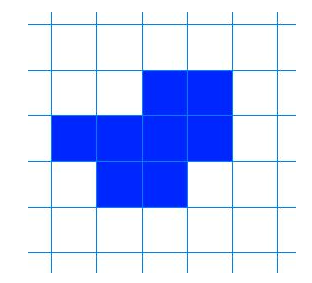
Vis fram en enkel figur laget av kvadrater i et rutenett, for eksempel denne:
«Bruk et ruteark, og fargelegg kvadrater sånn at dere får en annen figur enn min, men med samme areal.»
«Min figur har omkrets 14. Har noen andre en figur med omkrets 14?»
Samle inn eksempler og vis dem fram.
«Har noen en figur med omkrets mindre enn 14?»
Vis fram eksemplene.
«Har noen en figur med omkrets større enn 14?»
Vis fram eksemplene.
Hvis noen av kategoriene ikke har eksempler i klassen, kan du utfordre elevene til å lage passende figurer.
«Areal og omkrets er to av kjennetegnene/egenskapene ved disse figurene. På dette bildet er robotene plassert etter kjennetegnene sine. Kan dere finne ut hvordan de er plassert?»
Trekk fram nøkkelideene:
Når du går fra venstre til høyre, øker bredden på roboten.
Når du går fra toppen til bunnen, øker høyden på roboten.
Alle robotene i den midterste kolonnen har samme bredde.
Alle robotene i den midterste raden har samme høyde.
Vis så fram bildet av robotene for å oppsummere det elevene (forhåpentligvis) har lagt merke til. Vis også rutenettet som de skal bruke i resten av aktiviteten.
«Vi kan plassere figurene i et rutenett på 3 x 3 på samme måte, ved å sortere dem etter areal og omkrets i stedet for etter høyde og bredde.»
Gi hvert elevpar kortene (se kopioriginalen med ni figurer) til den første utfordringen, vis rutenettet på tavla, og forsikre deg om at elevene vet hva de skal gjøre:
Når parene blir ferdige, kan de få det andre settet med kort (se kopioriginalen med ni rektangler) og arbeide på samme måte. De som blir fort ferdige, kan arbeide med et utvidet rutenett, som dette:
Mot slutten av timen samler du klassen og deler effektive måter elevene fant for å sammenligne areal og omkrets.
Når dere ser på tilbakemeldinger fra den første utfordringen, kan du spørre elevene om hva de la merke til om figurene i den øverste raden i rutenettet.
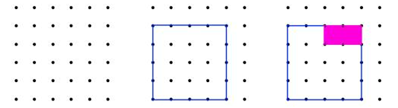
For å forklare hvorfor omkretsen er 16 for alle figurer som tegnes ved å kutte hjørnene på et kvadrat som er 4 · 4, kan disse bildene være til hjelp:
«Hvor mye av omkretsen mister man når man kutter av det rosa rektangelet? Hvor stor omkrets får man?»
Figurer på den andre og tredje raden kan sammenlignes på samme måte.
Med den andre utfordringen vil vi få elevene til å innse dette:
«Rektangler som er nærmere kvadrater, har mindre omkrets enn lange, tynne rektangler med samme areal.»
Et spørsmål som kan trekkes ut fra dette, er:
«Hvis to rektangler har samme areal, hvordan kan jeg finne ut hvilket som har størst omkrets?»
Diskuter til slutt det mulige innholdet i de fire tomme rutene i det utvidede rutenettet, og fokuser særlig på hvorfor det er umulig å fylle enkelte av dem.
Mulig utvidelse
Elevene kan til slutt lage sitt eget sett med kort, der et rektangel med dimensjoner 1 · 5 er kortet i midten. Det tvinger dem til å vurdere rektangler med sidelengder som ikke er heltall.
Ressursen er utviklet av NRICH