Elleville mønster
Aktivitet
Mange har sikkert prøvd å lage mønster i 100-kartet (rutenettet med 10 x 10 ruter). Når vi bruker multiplikasjonstabellene som utgangspunkt for mønster, kan vi finne mønster med vertikale og diagonale linjer, og noen mønster som gjentar seg over hele rutenettet. I dette problemet vil vi kalle 100-kartet tier-kartet. Hvis kartet har 9 x 9 ruter, vil vi kalle det nier-kartet, osv.
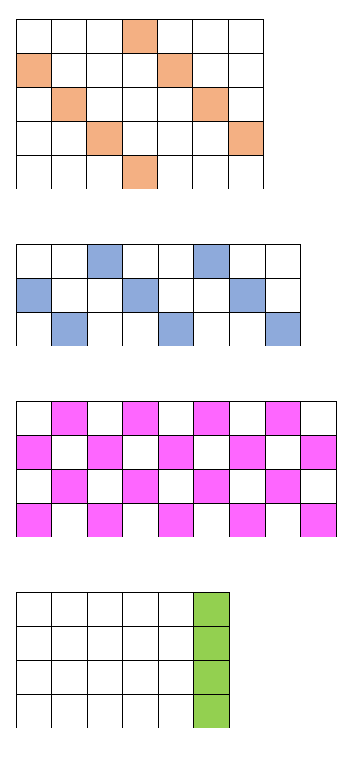
Hvilke tall kan ha laget mønstrene ovenfor?
Under finner du flere mønster, men her er det brukt fra firer-kart til nier-kart. Først er det laget mønster i et sjuer-kart, så i et femmer-kart, et åtter-kart og et sekser-kart. Hvilke tall er det som lager de ulike mønstrene? Kan du forklare hvorfor mønstrene blir slik i disse kartene?
Nå kan du utforske mønster selv. Du kan bruke dette rutearket når du eksperimenterer. Hvilke tall er det som lager diagonaler i de ulike kartene? Er det noen sammenheng mellom kartstørrelsen og tallene som lager diagonaler i de ulike kartene?
Hvilke tall er det som lager vertikale linjer i de ulike kartene? Er det noen sammenhenger her?
Prøv å lage noen av de andre mønstrene i andre kart. Hvilke mønster klarer du å lage, og i hvilke kart klarer du å lage dem?
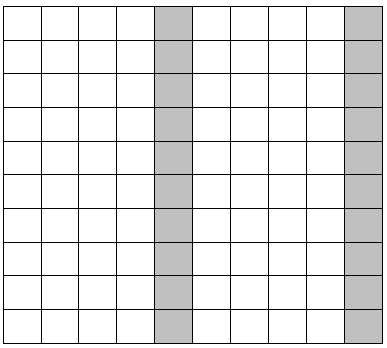
Nå er du kanskje klar for en større utfordring? Du får ikke se hele kartet, bare de øverste radene. Prøv å finne ut hvilket kart som er brukt, og hvilket tall som lager dette mønsteret. Det kan hende du trenger rutepapir for å løse oppgaven. Det finner du her.
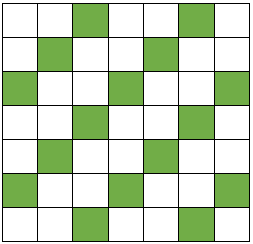
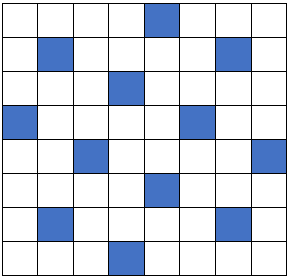
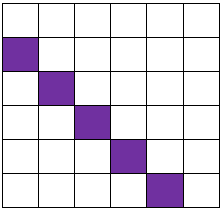
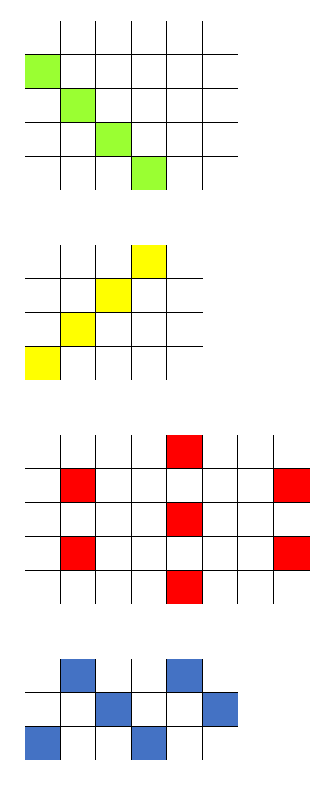
Nå kommer den største utfordringen! Klarer du å finne ut hvilke kart og hvilke tall som lager mønstrene under? Her får du se bare deler av kartene, og sidene på kartene vises ikke. NB! Det kan finnes mer enn én løsning.
Løsning
Omar og Peter sier at de har funnet ut følgende:
- Hvis det blir et mønster der hver fjerde rute er fargelagt, vil mønsteret inneholde multiplerMultippel er produktet av et gitt tall og et heltall. Tallet 8 en multippel av tallet 2, men også av 4, siden 8 er delelig med både 2 og 4. av 4, og hvis hver sjette rute er fargelagt, vil mønsteret inneholde multipler av 6, osv.
- I sjuer-kartet er hver tredje rute fargelagt, altså multipler av 3, så tallet 3 lager mønsteret.
- I femmer-kartet er annenhver rute fargelagt, og alle er multipler av 2. Derfor er det 2 som lager mønsteret. Vi fant også ut at på et oddetallskart (f.eks. sjuer-kart eller nier-kart) vil 2 lage et mønster som på et sjakkbrett, mens hvis det er et partallskart (f.eks. sekser-kart eller åtter-kart), vil 2 lage et mønster med vertikale linjer.
- I åtter-kartet er hver femte rute fargelagt (multipler av 5). Derfor er det 5 som lager mønsteret.
Bente og Pari har undersøkt når mønsteret blir diagonaler, og funnet ut følgende:
- I sekser-kartet blir det diagonaler når vi fargelegger med tallene 5 og 7. I sjuer-kartet blir det diagonaler når vi fargelegger med tallene 6 og 8. Derfor tror vi at blir det diagonaler når vi fargelegger tallene som er én mer eller én mindre enn antall ruter i kartet. Vi prøvde for nier-kartet etterpå, og da ble det diagonaler med tallene 8 og 10.
Kine og Lisa har undersøkt kartene som ikke har sidekanter, og de har funnet ut følgende:
- I det første kartet er det en diagonal som begynner på den andre linja, og det er i alle fall 6 ruter i kartet. Det betyr at tallet som lager mønsteret, må være én større enn kartet. Vi tror derfor at kartet kan være et sekser-kart eller større, og at tallet som lager mønsteret, er én mer enn kartstørrelsen.
- Det andre mønsteret lager en diagonal som går andre veien. Derfor tror vi at tallet som lager dette mønsteret, er én mindre enn kartstørrelsen. Da kan kartet være et femmer-kart, og tallet som lager mønsteret, kan være 4.
- I det neste kartet lages mønsteret i hver sjette rute. Derfor må tallet som lager mønsteret, være 6. Hvis vi skal klare å lage dette mønsteret med 6, må det være et 15-kart.
- I det siste mønsteret fargelegges hver tredje rute. Det betyr at tallet som lager mønsteret, må være 3. Mønsteret blir forskjøvet én rute mot høyre for hver rad. Vi får til å tegne mønsteret i et åtter-kart. Kartet kan også utvides med 3, eller med multipler av 3. Mønsteret kan derfor tegnes i 8-kart, 11-kart, 14-kart, 17-kart, 20-kart, 23-kart osv.
Lærerveiledning
Hvorfor arbeide med denne oppgaven?
Arbeid med dette problemet kan øke elevenes forståelse av faktorer og multipler. Det kan også være et spennende arbeid som gir bedre forståelse av multiplikasjon. Elevene kan lage hypoteser og prøve dem ut. Aktiviteten kan dessuten gi mulighet til å introdusere ideen om at en bokstav kan stå for et hvilket som helst tall.
Elevene kan også få økt forståelse av mønster og design.
Mulig tilnærming
Arbeidet med dette problemet kan begynne med at elevene fargelegger mønster ut fra gangetabellene i et vanlig 100-kart. Det er viktig at mønstrene ikke alltid blir rette linjer, så elevene kan godt fargelegge 3-gangen og 4-gangen før de tar 2-gangen og 5-gangen. Spør hvorfor 2-gangen og 5-gangen blir rette linjer. Bruk ordet faktor når det er hensiktsmessig.
Hvis elevene allerede har gjort en del av slikt arbeid, kan du snakke om hva som danner rette linjer, og hvorfor. Gi elevene deretter et unummerert tier-kart (10 x 10 ruter). Du finner det i menyen til venstre. Be ulike læringspar fargelegge ulike gangetabeller i tier-kartet. Be dem prøve å forutse hvilket mønster det vil bli, før de fargelegger. Elevene kan i stedet krysse ut de rutene som danner mønsteret, for fargelegging kan ta for lang tid.
Nå kan dere se på de ulike kartene. Elevene kan arbeide i par og dele ideer, funn og refleksjoner.
Det finnes to kopioriginaler med ulike kart og mønster. Disse kopioriginalene har flere kart enn i oppgaven som ligger på nettet. På kopioriginal A ligger det et kart til første del av oppgaven, og på kopioriginal B finnes det utsnitt av kart der sidekantene mangler. Oppgavene i B er mer krevende enn oppgavene i A, og de kan ha flere riktig svar. Ruteark kan være nødvendig når elevene skal arbeide med disse oppgavene.
Mot slutten av undervisningsøkta kan elevene forklare hvordan ulike mønster oppstår i ulike kart. Diskuter faktorene i tallet som beskriver størrelsen på kartet. Det bør dere også gjøre med tallene som er én mer og én mindre. I denne forbindelsen kan du innføre en bokstav som står for et hvilket som helst tall.
Elevene kan dessuten diskutere hva som skaper spennende mønster som fyller store deler av kartene.
Gode veiledningsspørsmål
- Hvilket mønster tror dere at dere vil få her?
- Hvilke tall gir vertikale linjer? Hvorfor tror dere det er sånn?
- Hvilke tall danner diagonaler? Hvorfor gjør de det?
- Hvilke typer kart og tall tror dere danner sjakkrutemønster?
- Hva er det som danner spennende mønster som fyller store deler av kartene?
Mulig utvidelse
Elever som blir tidlig ferdige og har gode forklaringer på svarene sine, kan lage lignende oppgaver til medelevene sine.
Elevene kan prøve å forutse og arbeide i sjuer-kart og tolver-kart. De kan også forsøke å uttrykke funnene sine algebraisk.
Mulig støtte
La elevene bruke et nummerert 100-kart og undersøke mønster i det.
Ressursen er utviklet av NRICH