Nedenfor ser du en tabell med tallene 1 – 100, et «hundrekart».
Fire ruter som danner et kvadrat, er markert med rødt. Bruk de fire tallene til å lage et regnestykke etter et bestemt mønster:
Tallene som danner en diagonal fra øvre høyre til nedre venstre hjørne multipliseres med hverandre. Trekk så ifra produktet av tallene i den andre diagonalen.
I de røde rutene blir regnestykket: \(2\cdot 11-1\cdot 12\)
Hva ble svaret?
Så velger du kvadratet med de fire lyseblå rutene og lager et regnestykke etter samme mønster. Hva ble svaret der?
Velg flere kvadrater med fire ruter på andre steder i hundrekartet og gjør tilsvarende utregning. Hva blir svaret?
Du finner et hundrekart som kan skrives ut her. Du kan legge brikker i rutene for regnestykkene du lager, slik at arket kan brukes flere ganger.
Hva er sammenhengen mellom svarene du får? Hvorfor blir det slik?
Fortsett med å undersøke regnestykker du får ved å markere kvadrater i hundrekartet, slik vi har vist med 3 x 3-ruter, 4 x 4 -ruter osv. slik figuren antyder. Bruk tallene i hjørnene. Marker kvadrater av samme størrelse flere steder i hundrekartet og regn hele tiden etter samme mønster som ovenfor.
Et skjema kan være til hjelp:
| Størrelsen på kvadratet som markeres |
Svaret på regnestykket som er laget av tallene i hjørnene etter mønsteret: |
| 2 x 2 | |
| 3 x 3 | |
| 4 x 4 | |
| 5 x 5 | |
| 6 x 6 | |
| 7 x 7 | |
| 8 x 8 | |
| 9 x 9 | |
| 10 x 10 |
Fant du et mønster som var slik at du visste hva som ble svarene for kvadratene du ikke hadde regnet ut? Kan du beskrive mønsteret? Kan du forklare hvorfor det blir slik?
Du kan markere figurer som ikke er kvadrater, lage en regneregel og undersøke om du kan finne flere mønster i hundrekartet.
Hva vil du undersøke?
Legg en plan, hvilke figurer kan du lage i stedet for kvadrater? Hvilken regneregel skal gjelde? Undersøk systematisk. Finner du flere mønster? Kan du forklare hvorfor mønstrene blir som de blir? Kan du være sikker på at mønstrene du velger, vil gi de samme svarene uansett hvor i hundrekartet du markerer figuren?
I denne oppgaven skal elevene først eksperimentere og finne mønstre. Det er en fin oppgave for å vise hvordan vi generaliserer ved hjelp av algebra.
La elevene samarbeide i par.
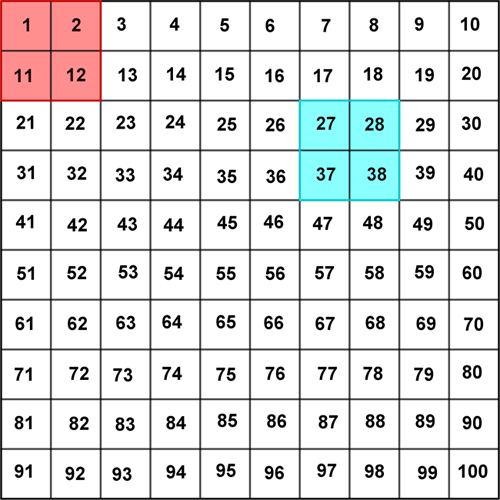
La dem få et «hundrekart» å arbeide med, det finnes på kopioriginal her sammen med tellebrikker eller noe som kan legges som markering i rutene på arket. Be elevene markere de fire rutene som danner et 2 x 2-kvadrat øverst i venstre hjørne (1, 2, 11, 12) og be dem regne etter mønsteret som er angitt i oppgaven: \(\text{øvre høyre}\cdot\text{nedre venstre}-\text{øvre venstre}\cdot\text{nedre høyre}\).
Sørg for at alle forstår hvordan vi setter opp regnestykket, for det skal de bruke mange ganger i denne aktiviteten. Hva blir svaret? Fikk alle det samme?
Be elevene fortsette med å markere rutene 27, 28, 37, 38 og regne ut på tilsvarende måte her. Hva blir svaret nå? Er det noen som tror de kan finne flere steder i hundrekartet hvor de vil få samme svar? La dem prøve en stund (bare med 2 x 2-ruter). Når alle har fått tid til flere forsøk, er det tid for å diskutere i fellesskap: Vil det bli samme svar uansett hvor vi plasserer kvadratet?
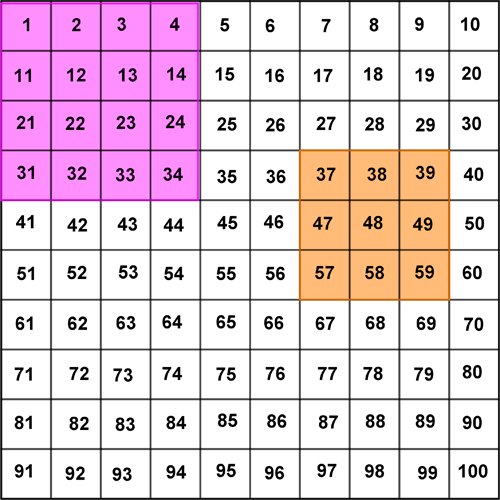
Kan noen forklare hvorfor? Slipp til alle forklaringer de kan komme med, men la det i første omgang stå åpent hva som er rett og galt. Nå skal elevene tas med i tenkningen som ligger bak en generalisering: Be dem markere 2 x 2-kvadrater på to ulike steder i hundrekartet:
Se på de to øverste tallene i de to markerte feltene: Hva er likt, hva har de til felles? Kan alle se at uansett hvor de markerer vil det andre tallet være 1 større enn det første?
Nå kan du innføre bokstaver for tall: Velg en bokstav, for eksempel a. Hvis tallet øverst til venstre i ruta er a, hva er da tallet øverst til høyre? (a + 1)
Så kan de sammenligne de to markerte kvadratene på nytt, se på tallene øverst til venstre og nederst til venstre: Har disse to tallene noe til felles i de to markerte rutene? Kan alle se at uansett hvor vi plasserer et 2 x 2-kvadrat vil det nederste tallet være 10 større enn det øverste? Hvordan kan vi skrive dette tallet på algebraspråket? (a + 10)
Hvordan kan vi da skrive tallet nederst til høyre i 2 x 2-kvadratet? Få alle med på at dette blir a + 11.
Det betyr at alle 2 x 2-kvadrater kan skrives på samme måte:
| \(a\) | \(a+1\) |
| \(a+10\) | \(a+11\) |
Skriv dette opp på tavla og be elevene regne ut etter samme mønster som før. Hva ser de? Hva blir svaret?
Nå kan dere gå tilbake til forklaringene elevene hadde kommet med: Var de i samsvar med det vi gjorde her? Var noe forskjellig, evt. hva? Var det noen som ønsket å endre forklaringen sin fordi de hadde misforstått noe? Hva hadde de misforstått?
Hvis dere arbeider grundig med denne første delen av oppgaven, kan elevene arbeide mer selvstendig med fortsettelsen: Marker kvadrater med andre størrelser i hundrekartet, 3 x 3, 4 x 4 osv. Be dem notere størrelsen på kvadratene og svaret på utregningene, bruk alltid tallene i hjørnene av kvadratene og følg samme regel som før. Kan de finne et system i svarene ettersom de gjør kvadratene gradvis større? Kan de finne en forklaring på hvordan disse svarene utvikler seg? Kan de finne en generell sammenheng eller regel?
Bruk tid på å oppsummere og ha spesielt fokus på generaliseringene. Sørg for at de kan forklares både med ord og med symboler.
I det videre arbeidet er det åpent for mer utforskning. Elevene kan komme med forslag til hva slags figurer i hundrekartet de vil utforske og hva regneregelen skal være. Det enkleste er nok å fortsette med rektangler. Dere kan enten bli enige om én oppgave som alle arbeider videre med, eller du kan la hvert arbeidspar arbeide med egne ideer. I så fall må de lage en skriftlig rapport som forteller hvilken figur de har valgt i hundrekartet, hva som er regneregelen deres, hvilke eksempler på utregning de har prøvd og hvordan de har generalisert resultatet. Det kan hende noen lager figurer og regneregler som ikke gir samme svar gjennom hele hundrekartet. I tilfelle er det en fin oppgave å utfordre elevene til å finne ut hvorfor. Det er fint om slike rapporter over arbeidet i de enkelte parene kan bli synlige for alle til slutt.
Oppgaven kan utvides i mange retninger idet man lar elevene selv velge figurer i hundrekartet som skal utforskes, og hvilke regneregler som skal gjelde.
Ressursen er utviklet av Matematikksenteret
