Magiske bokstaver
Aktivitet
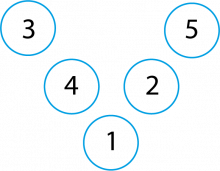
Charlotte har laget en magisk V med fem påfølgende tall:
Det er en Magisk V, for når du legger sammen tallene i hver «arm» får du den samme summen.
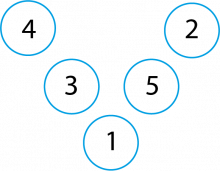
Arne tegnet en slik Magisk V:
Charlotte sa: «Det er egentlig den samme som min Magiske V!»
Hva tror du Charlotte mente med dette?
- Kan du finne alle mulige Magiske V’er som bruker tallene 1 til 5 som er forskjellige fra Charlotte sine?
- Hvordan kan du være sikker på at du har funnet alle?
- Hva skjer om du bruker tallene fra 2 til 6?
- Eller fra 3 til 7?
- Eller 4 til 8…?
Her er et regneark som kan hjelpe deg med å undersøke Magiske V’er med fem påfølgende tall.
- Kan du beskrive en effektiv strategi for å finne alle magiske V’er for fem hvilke som helst påfølgende tall ?
- Kan du bruke din strategi til å finne alle mulige magiske V’er som bruker tallene 987, 988, 989, 990, 991?
- Kan du finne en Magisk V der hver «arm» har sum lik 60? Eller 1000? Eller…?
Kan du finne mer enn én?
Kan du finne en Magisk V for alle mulige «armsummer»?
Charlotte og Arne tegnet noen flere bokstaver, for å se om de kunne gjøre dem magiske; dvs. å bruke påfølgende tall for å lage like summer på «armene». Magisk L, N og W:
- Utforsk noen av disse magiske bokstavene på samme måte som du utforsket den magiske V.
- Kan du finne noen generelle konklusjoner?
Du kan bruke dette regnearket til å utforske magiske L, N og W.
Starthjelp
Hva legger du merke til når det gjelder tallet som står nederst i de magiske V’ene?
Løsning
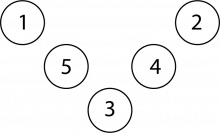
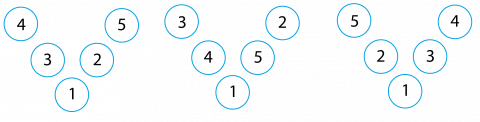
Det er seks mulige løsninger av magisk V når vi bruker tallene fra 1-5 og lar 1 stå nederst. Alle disse er samme løsning som Charlotte sin:
Siden summen av tallene 1 + 2 + 3 + 4 + 5 = 15, må et oddetall stå nederst. Hvis vi setter et oddetall nederst, vil summen av de øvrige tallene bli et partall, og det kan deles i to like summer. Men hvis vi setter et partall nederst, vil summen av de øvrige tallene bli et oddetall som aldri kan deles i to like tall.
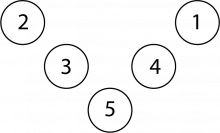
Hvis vi setter 3 nederst får vi en løsning som kan ordnes på seks ulike måter slik som i eksempelet ovenfor med 1 nederst:
Hvis vi setter 5 nederst får vi en løsning som også kan ordnes på seks ulike måter slik som i eksempelet ovenfor:
Lærerveiledning
Hvorfor arbeide med denne oppgaven?
Denne oppgaven gir elevene øving i å oppfatte en struktur i et enkelt tilfelle og generalisere løsningene ut fra strukturene de har funnet.
Mulig tilnærming
Begynn med å tegne 5 sirkler slik at de danner en V og be elevene gjøre det samme og prøve å plassere tallene 1-5 i hver sin sirkel. De kan sette tallene i de sirklene de selv ønsker.
La elevene vise fram løsningene sine og del tavla i to, med overskriftene «Magisk» og «Ikke magisk». Velg noen av løsningene som elevene har laget, og tegn dem opp på tavla i de to ulike kategoriene uten å fortelle hva som gjør noen «magiske» og andre ikke. Utfordre elevene til å finne ut hva som gjør en løsning «magisk».
Når elevene har funnet ut hva som gjør en V «magisk», må det gjøres klart hva som gjør to løsninger ulike, og hvorfor for eksempel de tre løsningene nedenfor er like:
Arbeid til dere har funnet alle mulige løsninger (det er tre ulike løsninger, med hhv. 1, 3 eller 5 nederst).
Ta dere tid til å diskutere hvorfor dere kan være sikre på at det ikke finnes flere løsninger. Hva skjer når det står et oddetall nederst i V’en, og hva skjer når det står et partall?
La elevene nå løse en tilsvarende oppgave med tallene 2-6. Kan de bruke samme strategi som fungerte i den første oppgaven? Kom med gode veiledningsspørsmål som hjelper elevene på veien til å løse problemet selv.
Legg merke til elever som finner effektive løsningsstrategier. La dem få vise sine strategier og forklare hvordan de har tenkt.
La elevene fortsette å arbeide i par med flere magiske V’er:
- Bruke tallene fra 3 til 7
- Bruke tallene fra 4 til 8
- Kan du beskrive en effektiv strategi for å finne alle magiske V’er for fem hvilke som helst påfølgende tall?
- Kan du bruke din strategi til å finne alle mulige magiske V’er som bruker tallene 987, 988, 989, 990, 991?
- Kan du finne en Magisk V der hver «arm» har sum lik 60? Eller 1000? Eller…?
Kan du finne mer enn én?
Kan du finne en Magisk V for alle mulige «armsummer»?
Gode veiledningsspørsmål
- Hva ble summen langs hver side når vi brukte tallene 2-6?
- Hvorfor blir summen langs hver side av V med 2 i bunnen 3 større enn om vi har 1 i bunnen?
- Hva er spesielt med summen langs hver side hvis tallet i bunnen er det midterste av fem påfølgende tall?
Her finner du en kopioriginal, en side med magisk V og en side med magisk L, N og W.
Her finner du regneark for å utforske Magisk V.
Mulig utvidelse
Oppgaven kan utvides med Magisk L, N og W. De kan utforskes på tilsvarende måte. Ha fokus på å finne gode strategier.
Her finner du regneark for Magisk L, N og W.
Ressursen er utviklet av NRICH