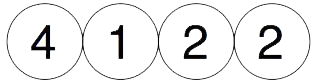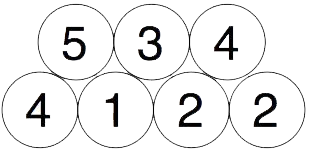Talltårn
Aktivitet
Vi starter med fire tilfeldige tall, men ikke 0.
Så legger vi sammen tallene parvis og plasserer de nye tallene over, slik:
Deretter legger vi sammen de nye tallene parvis og plasserer de nye tallene over på samme måte, slik:
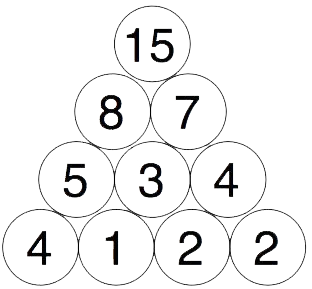
Til slutt legger vi sammen de to siste tallene og plasserer det siste tallet på toppen, slik:
- Velg fire nye tall som gjør at tallet på toppen blir 15.
- Finn så mange eksempler på fire starttall du greier, som gjør at tallet på toppen blir 15.
- Finner du et system? Kan du beskrive det?
- Hvor kan det lønne seg å starte?
Løsning
Å starte med de fire nederste tallene gjør det vanskelig å vite hvilke tall som gjør at vi ender opp med 15 på toppen. Det lønner seg å starte på toppen av tårnet og finne ut av hvilke to tall som til sammen gir 15. Disse tallene er
14 + 1 , 13 + 2 , 12 + 3 , 11 + 4 , 10 + 5 , 9 + 6 , 8 + 7 , 7 + 8 , 9 + 6 , 5 + 10 , 4 + 11 , 3 + 12 , 2 + 13 , 1 + 14
Ettersom to hele tall ikke kan gi 1 til sum, kan vi fjerne 1 + 14 og 14 + 1. På samme måte kan vi også ta bort 2 + 13 og 13 + 2 fordi de bare kan gi 12, 1, 1 på tredje rekke. 1 i tredje rekke gjør det ikke mulig å lage en fjerde rekke.
Vi kan sette tallene inn i en tabell og se hvor mange ulike kombinasjoner det blir i nest nederste rad.
|
Sum 15 |
|
|
|
|
|
|
|
12 + 3 |
11, 1, 2 |
10, 2, 1 |
|
|
|
|
|
11 + 4 |
10, 1, 3 |
9, 2, 2 |
8, 3, 1 |
|
|
|
|
10 + 5 |
9, 1, 4 |
8, 2, 3 |
7, 3, 2 |
6, 4, 1 |
|
|
|
9 + 6 |
8, 1, 5 |
7, 2, 3 |
6, 3, 2 |
5, 4, 3 |
4, 5, 1 |
|
|
8 + 7 |
7, 1, 6 |
6, 2, 5 |
5, 3, 4 |
4, 4, 3 |
3, 5, 2 |
6, 2, 1 |
|
7 + 8 |
3, 4, 5 |
5, 2, 6 |
6, 1, 7 |
|
|
|
|
6 + 9 |
3, 3, 6 |
2, 4, 5 |
1, 5, 4 |
4, 2, 7 |
|
|
|
5 + 10 |
4, 1, 9 |
3, 2, 8 |
2, 3, 7 |
1, 4, 6 |
|
|
|
4 + 11 |
3, 1, 10 |
2, 2, 9 |
1, 3, 8 |
|
|
|
|
3 + 12 |
1, 2, 10 |
2, 1, 11 |
|
|
|
|
Alle kombinasjonene som gir 1 i nest nederste rad, tar vi bort. I tillegg er 3, 5, 2 og 2, 5, 3, som blir 8, 7 og 7, 8 i nest øverste rad, en umulig kombinasjon å lage. Den eneste muligheten vi har for å lage 2, er 1, 1. Det betyr at 5 lages av 1 og 4, men 4 er et høyere tall enn 3. Dette kan vises slik:
Da står vi igjen med dette:
|
Sum 15 |
|
|
|
|
|
11 + 4 |
9, 2, 2 |
|
|
|
|
10 + 5 |
8, 2, 3 |
7, 3, 2 |
|
|
|
9 + 6 |
7, 2, 3 |
6, 3, 3 |
5, 4, 2 |
|
|
8 + 7 |
6, 2, 5 |
5, 3, 4 |
4, 4, 3 |
|
|
7 + 8 |
3, 4, 5 |
5, 2, 6 |
4, 3, 5 |
|
|
6 + 9 |
3, 3, 6 |
2, 4, 5 |
4, 2, 7 |
|
|
5 + 10 |
3, 2, 8 |
2, 3, 7 |
|
|
|
4 + 11 |
2, 2, 9 |
|
|
|
Det gir følgende kombinasjoner med tallene i nederste rad:
|
Sum 15 |
Linje 3 |
Linje 4 |
|
11 + 4 |
9,2,2 |
8,1,1,1 |
|
10 + 5 |
8,2,3; 7,3,2 |
7,1,1,2; 5,2,1,1 |
|
9 + 6 |
7,2,4; 6,3,3; 5,4,2 |
6,1,1,3; 5,1,2,1; 4,2,1,2; 2,3,1,1 |
|
8 + 7 |
6,2,5; 5,3,4; 4,4,3; |
5,1,1,4; 4,1,2,2; 3,2,1,3; 2,2,2,1; 1,3,1,2 |
|
7 + 8 |
4,4,3; 4,3,5; 5,2,6 |
1,2,2,2; 2,1,3,1; 4,1,1,5; 2,2,1,4; 3,1,2,3 |
|
6 + 9 |
3,3,6; 2,4,5; 4,2,7 |
1,2,1,5; 2,1,2,4; 1,1,3,2; 3,1,1,6 |
|
5 + 10 |
3,2,8; 2,3 7 |
2,1,1,7; 1,1,2,5 |
|
4 + 11 |
2,2,9 |
1,1,1,8 |
Lærerveiledning
Hvorfor arbeide med denne oppgaven?
Denne oppgaven utfordrer elevene til å være kreative matematikere. De må lete etter mønster og systemer, lage hypoteser og kontrollere dem, og de må bruke det de allerede kan, i nye sammenhenger. Kreative matematikere prøver seg fram med eksempler, tegner, eksperimenterer og stiller gode spørsmål.
Mulig tilnærming
Denne aktiviteten fungerer både i individuelt arbeid og som gruppearbeid, men vi anbefaler at elevene får mulighet til å dele og diskutere løsninger med hverandre.
En måte å organisere aktiviteten på er å introdusere oppgaven felles for alle elevene, for eksempel på smartboard. Det er viktig at de noterer ned svarene de finner og strategiene de bruker. Kopieringsoriginaler til å fylle ut tall finner du her PDF.
Etter at elevene har arbeidet en stund med oppgaven, bør de få mulighet til å diskutere med hverandre. Plasser dem i grupper på 2–3 elever. Hvis de allerede har arbeidet i grupper, kan du la dem diskutere videre. Veiledningsspørsmålene kan være til hjelp videre i arbeidet.
Sett av tid på slutten av timen til å løfte fram løsninger og strategier i plenum. Skriv dem opp slik at de blir tilgjengelige for alle elevene. Diskuter likheter og forskjeller i løsningene.
En diskusjon som kan dukke opp i gruppene og i plenum, er når to løsninger har like tall, bare på forskjellig plass, for eksempel:
Det er ikke et riktig eller feil svar i dette tilfellet, men det er et eksempel på at det ofte må bestemmes et kriterium for åpne oppgaver som denne.
Gode veiledningsspørsmål
- Hva har dere funnet ut? Har dere et system?
- Er det noe spesielt med de fire tallene nederst? Er det noen tall som går igjen? Hvorfor er det slik?
Mulig utvidelse
- Kan du lage tårn med andre regneregler? Hva skjer om det er lov å bruke 0? Hva med negative tall?
- Lag et tårn med 5, 6, 7 … tall nederst.
Ressursen er utviklet av NRICH