Lek i hagen med Mona og Anne-Mari
Aktivitet
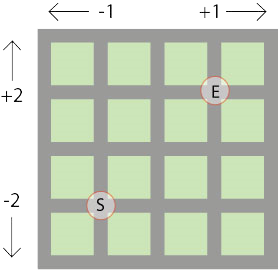
Mona og Anne-Mari liker å leke i hagen til bestemor. Hagen har mange stier med gress mellom, og ligner litt på bildet under.
En dag fant Mona og Anne-Mari opp en ny lek. Reglene er slik:
For hver gressflekk de løp forbi når de løp til høyre, måtte de legge til ett poeng.
For hver gressflekk de løp forbi når de løp til venstre, måtte de trekke fra ett poeng.
For hver gressflekk de løp forbi når de løp til framover, måtte de legge til to poeng.
For hver gressflekk de løp forbi når de løp til bakover, måtte de trekke fra to poeng.
Mona og Anne-Mari startet på punktet S og sluttet på punktet E på bildet under. De hadde 10 poeng da de startet, og la til og trakk fra poeng etter hvert som de valgte en vei til punktet E.
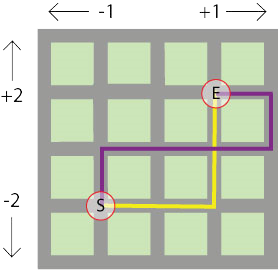
Her ser du hvilke veier de tok.
Mona valgte den lilla løypa, mens Anne-Mari valgte den gule løypa.
Hvor mange poeng hadde Mona da hun kom fram til punktet E?
Hvor mange poeng hadde Anne-Mari da hun kom fram til punktet E?
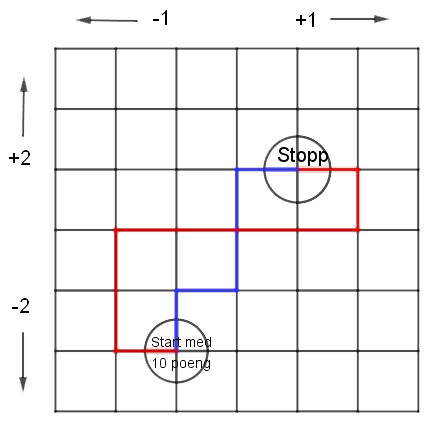
Nedenfor har vi tegnet et ruteark. Vi har tatt bort gresset og veiene, men vi tenker oss at de hvite kvadratene er gresset, og at strekene er veiene.
Vi har tegnet inn to nye veier, en rød og en blå.
Hvor mange poeng vil du ha til slutt hvis du velger den røde veien?
Hvor mange poeng vil du ha til slutt hvis du velger den blå veien?
Lag noen nye veier, og regn ut hvor mange poeng du har igjen for hver rute du lager. Legger du merke til noe spesielt? Kan du forklare hvorfor det blir slik?
Du kan laste ned kopioriginal av rutearket her.
Starthjelp
- Forsøk å gå veien selv med en brikke. Start med 10 poeng. Gjør utregninger for hvert steg du tar underveis, for at det skal bli lettere holde orden på poengsummen.
- Hvordan kan du holde orden på veiene du har gått, så du ikke glemmer hvor du har gått?
- Hvordan skal du holde orden på poengsummen for hver gang?
Løsning
Den lilla løypa gir følgende regnestykke: 10 + 2 + 1 + 1 + 1 + 2 – 1 = 16
Den gule løypa gir følgende regnestykke: 10 + 1 + 1 + 2 + 2 = 16
Både Mona og Anne-Mari hadde 16 poeng da de kom fram. Det hadde ikke noe å si hvilken vei de tok.
Den røde løypa gir følgende regnestykke: 10 – 1 + 2 + 2 + 1 + 1 + 1 + 1 + 2 – 1 = 18
Den blå løypa gir følgende regnestykke: 10 + 2 + 1 + 2 + 2 + 1 = 18
En annen løype kan for eksempel være slik: 10 – 2 + 1 + 1 + 2 + 1 + 1 + 2 + 2 + 2 – 1 – 1 = 18
Det spesielle er at poengsummen blir den samme, uansett hvilken vei du går, så lenge startpunktet og sluttpunktet er det samme.
Det er ikke mulig å få et annet tall enn 18 fordi den korteste veien fra start til mål er 2 til høyre og 3 opp, som gir svaret 18 (10 + 1 + 1 + 2 + 2 + 2 = 18). Alle andre veier har en eller flere lengder som vil utligne hverandre. Tar du for eksempel ett steg bort fra målet (nedover), må du en eller annen gang ta steget tilbake (oppover), og da vil de to regnestykkene nulle hverandre ut. Derfor vil alle veier, uansett hvor kompliserte de er, føre til poengsummen 18.
Lærerveiledning
Hvorfor arbeide med denne oppgaven?
Denne aktiviteten vil gi elevene mulighet til å generalisere og lage hypoteser om hva som kommer til å skje, og hvorfor. Aktiviteten gjør også at elevene får øving i enkel addisjon og subtraksjon. Den synliggjør de inverse relasjonene mellom de to operasjonene, og motiverer elevene til å tenke på operasjonenes rekkefølge.
Mulig tilnærming
Her kan du hente en kopieringsoriginal til aktiviteten.
En måte å introdusere oppgaven på er å vise det første bildet til hele klassen på en smartboard, for å være sikker på at alle elevene forstår leken som Mona og Anne-Mari har laget. Hvis det er mulig, kan hagen med stiene og gresset lages med tape i klasserommet, eller i skolegården, så elevene kan gjøre leken selv.
Etter introduksjonen kan elevene arbeide sammen i par med oppgavene på en kopieringsoriginal. Når de arbeider i par, får de mulighet til å diskutere løsningsforslagene sine med hverandre. Oppfordre elevene til å lage forskjellige løyper med både addisjon og subtraksjon. De kan tegne inn rutene med ulike fargeblyanter, men det kan bli mange ruter, så de kan komme til å trenge flere kopieringsoriginaler. For noen elever kan det være nyttig å ha konkreter tilgjengelig når de skal addere og subtrahere poeng.
Når elevene har arbeidet med oppgavene, kan elevparene dele løsningene og strategiene sine i plenum. De kan vise de mest interessante og lengste rutene, og hva de har lagt spesielt merke til. Utfordre elevene på om det er noen som kan forklare hvorfor det blir den samme poengsummen, uansett hvilken rute man velger, så lenge startpunktet og sluttpunktet er det samme.
Gode veiledningsspørsmål
- Hvordan kan du holde styr på hvilke ruter du har prøvd ut?
- Hvordan skal du huske poengsummen for hver rute du prøver?
- Kan du finne en mer spennende vei å gå?
- Kan du sjekke poengsummen på en annen måte?
- La du merke til noe spesielt med den totale poengsummen?
Ressursen er utviklet av NRICH