Produkt-sudoku
Aktivitet
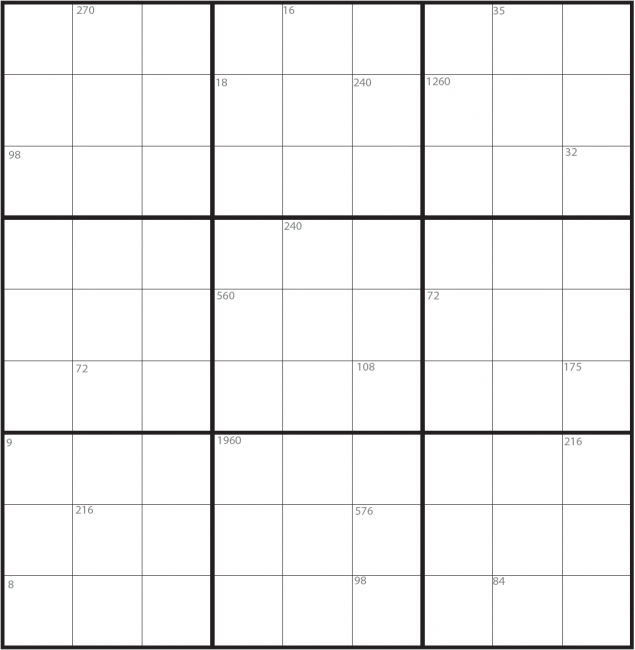
Sudoku #1
Reglar
På same måte som vanleg sudoku har produkt-sudoku to basisreglar:
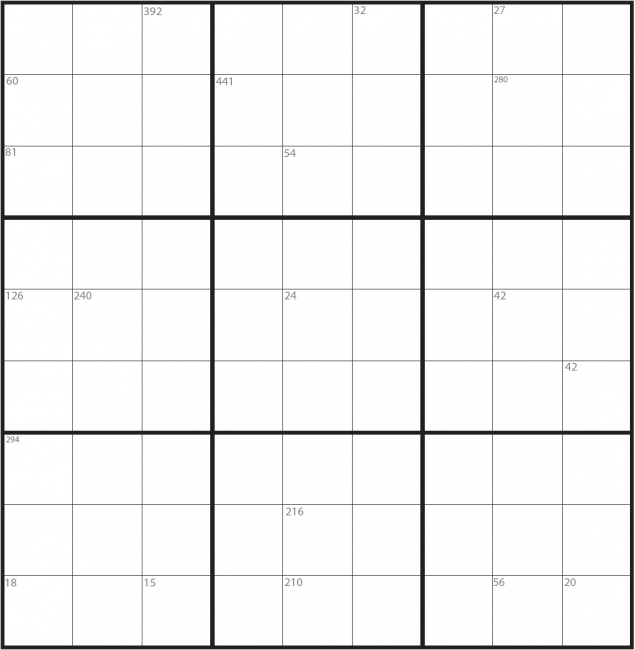
- Kvar kolonne, kvar rad og kvart 3 x 3-kvadrat skal innehalde tala 1–9.
- Ingen kolonne, rad eller 3 x 3-kvadrat kan ha same tal to gonger.
Produkt-sudoku kan løysast ved å bruke tala som er øvst i nokre av dei små rutene. Desse tala er produktet av tala som skal liggje i rutene ved sida av, vertikalt og horisontalt. Til dømes er 600 produktet av tala i dei raude rutene:
Nedanfor finn du fem andre brett. Du finn dei også som kopioriginalar.
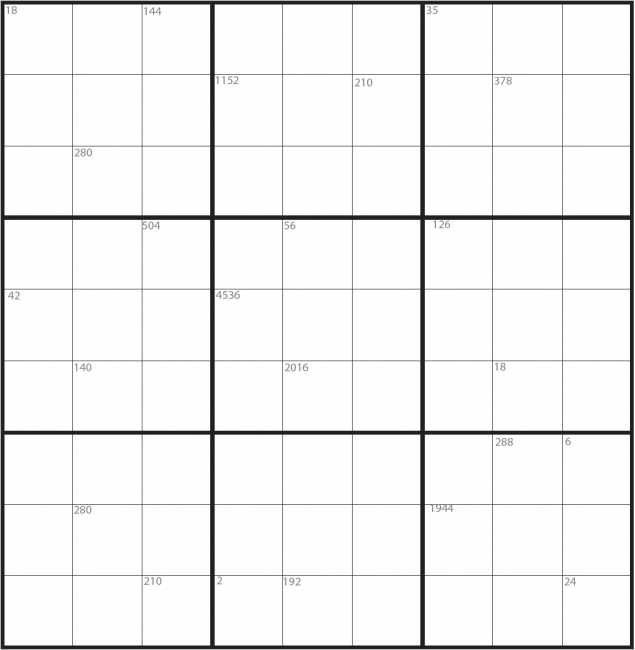
Sudoku #2
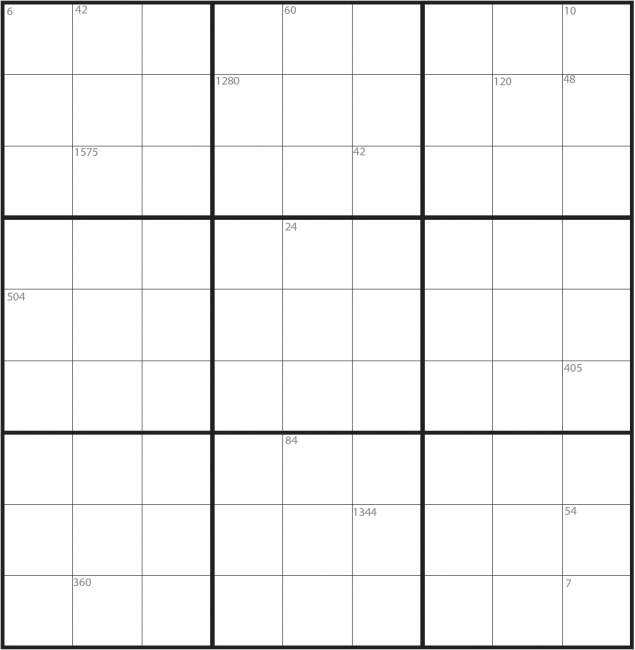
Sudoku #3
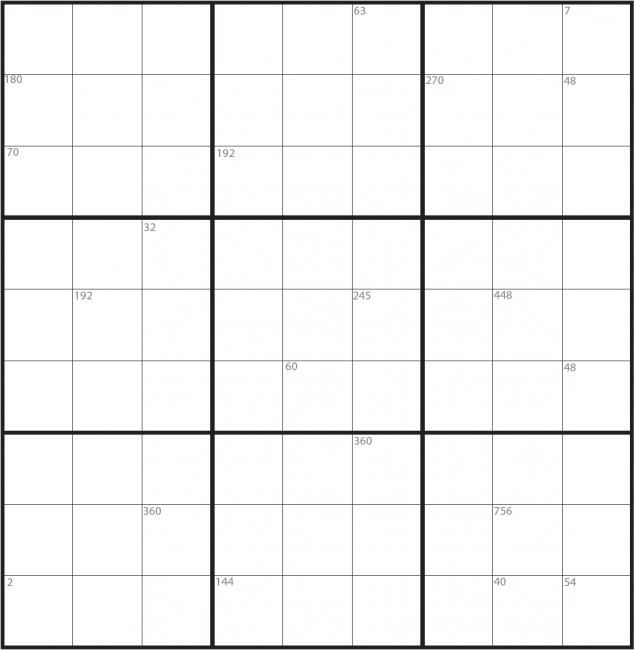
Sudoku #4
Sudoku #5
Sudoku #6
Starthjelp
Dette er ei oversikt over kva rekkjefølgje ein kan gå fram i når ein skal finne tala. Denne rekkjefølgja er ikkje den einaste som finst, berre ein av fleire moglege måtar å gjere det på. Byrj med å finne ut kva tal som skal stå i rute nr. 1, så i rute nr. 2, osb.
Lærarrettleiing
Kvifor arbeide med denne oppgåva?
Denne forma for sudoku utfordrar den matematiske kompetansen til elevane både når det gjeld logisk tenking, multiplikasjon og talforståing. Aktiviteten legg til rette for at elevane kan utvikle betre forståing av faktor, multiplikative tal og primtalsfaktorisering.
Mogleg tilnærming
Kopioriginalane i menyen til venstre kan vere nyttige.
Dersom elevane ikkje kjenner til den vanlege forma for sudoku, bør du setje av litt tid til å forklare dei det.
Vis elevane bretta til «produkt-sudoku» utan å forklare noko, og fyll inn dei to første tala. Sei at du vil fylle inn nokre tal til, og be elevane om å komme med forslag. Det er viktig at dei ikkje røper korleis systemet fungerer, viss dei finn det ut. Tittelen på oppgåva kan kanskje vere til hjelp.
Skriv inn forslaga frå elevane, og be dei om å grunngi forslaga sine. Hald fram til du meiner at dei har forstått samanhengen. Lever ut kopiar til dei som ønskjer å fullføre arket på eiga hand etter timen.
Sett elevane saman i par, og gi dei ein kopi av «produkt-sudoku» og skjemaet der dei kan notere rekkjefølgja av tala. Forklar at denne oppgåva er litt meir utfordrande enn den førre, og at det er viktig at dei skriv ned rekkjefølgja av tala dei finn. Når dei har funne eit tal, skal dei overtyde kvarandre om at forslaget deira er rett.
Etter kvart som elevpara blir ferdige, hengjer dei opp skjemaet som viser i kva rekkjefølgje dei fann tala, slik at alle saman ser og kan samanlikne. Samle elevane på slutten av timen, og be dei sjå etter likskapar og forskjellar mellom dei ulike skjemaa.
Gode rettleiingsspørsmål
Nokre av tala som er oppgitt, gjer at det kan vere mange moglegheiter, medan med andre tal kan det ikkje vere så mange moglegheiter. Kva tal er det lettast å byrje med, og kva er det vanskelegast å byrje med?
Mogleg utviding
Eit elevpar kan bruke eit anna elevpars skjema eller oversikt over rekkjefølgja dei fann tala i, og prøve å følgje same rute.
Elevsvar
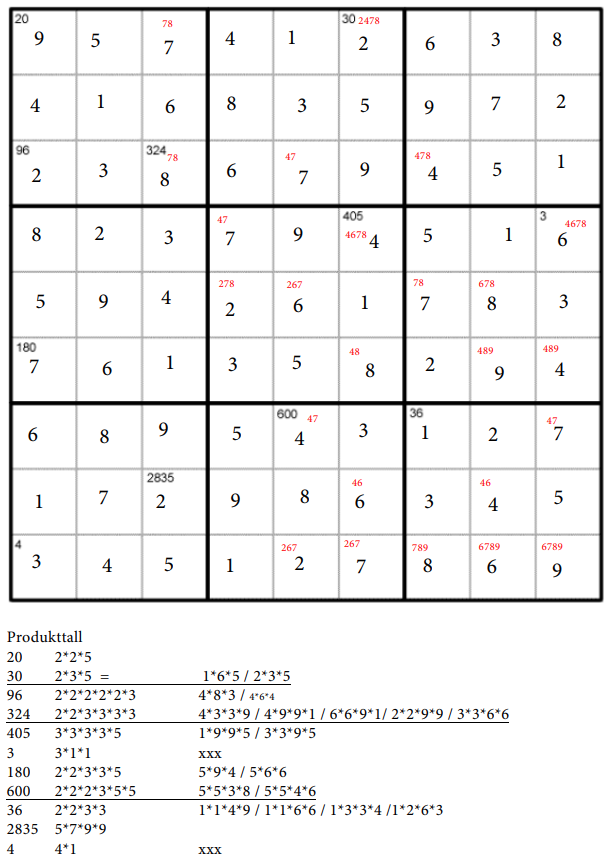
Line tok utfordringa på heimeskule og løyste det første brettet på følgjande måte:
Eg starta med å finne moglege faktorar til alle produkttala. Deretter om nokre nærliggjande produkttal hadde like faktorar:
Ressursen er utviklet av NRICH