Meir brøkstavar
Aktivitet
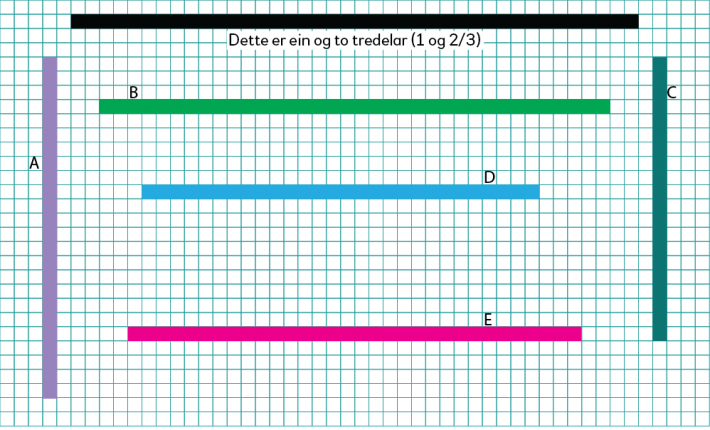
Sjå på dei forskjellige fargelagde stavane:
Du kan laste ned og skrive ut biletet frå lista med kopioriginalar til venstre.
Sorter stavane etter storleik. Kan du gjere det utan å klippe dei ut?
Sjå nærare på denne staven:
Denne staven representerer ein heil og to tredelar, eller talet \(1\frac23\). Det kan vere enklare å sjå han for seg som ein stav som er sett saman av ein heil og ein som er to tredelar av han.
Vi ser på dei andre fargelagde stavane som brøkar av den svarte staven. Det vil seie at vi ser på dei som brøkar av \(1\frac23\).
Sjå på staven A (lilla) nedanfor.
For å gjøre det enklere å sammenligne stavene kan vi tegne linjer, slik:
Kor stor brøkdel av den svarte staven er staven A?
Samanlikn alle dei fargelagde stavane med den svarte staven.
Kor stor brøkdel av \(1\frac23\) er dei forskjellige stavane?
Skriv ned det du finn ut om kvar stav. Du kan for eksempel gjere det på denne måten:
Staven A er tre femdelar av den svarte staven.
eller:
Staven A er \(\frac35\) av \(1\frac23\).
eller:
Staven A representerer ein heil.
Kan du finne ut korleis vi kom på dei tre forslaga?
Kor stor del av \(1\frac23\) representerer kvar stav? Prøv å vise det på fleire måtar.
Lærarrettleiing
Kvifor arbeide med denne oppgåva?
Denne oppgåva gir elevane moglegheit til å arbeide med sortering og samanlikning av brøkar. Her møter dei ideen om ein brøkdel av ein brøk, i tillegg til ein brøkdel av ein heil. Gjennom samarbeid kan elevane utvikle vokabularet sitt knytt til brøk.
Mogleg tilnærming
Vis nokre stavar med forskjellig lengde på ein storskjerm eller ei interaktiv tavle. Set saman nokre kortare stavar slik at elevane ser at dei til saman blir like lange som ein større stav. Kan elevane forklare kor stor brøkdel ein av dei små stavane er av den store staven? Dersom den store staven utgjer \(1\frac23\), kor stor brøkdel representerer dei små då?
Elevane kan samarbeide i par eller grupper og lage dei forskjellige stavane av centikubar eller anna veleigna konkretiseringsmateriell. Eventuelt kan dei bruke utskrifter av kopioriginalen og klippe ut stavane. Det kan vere lurt at kvar elev eller gruppe lagar fleire kopiar av den same staven, slik at dei kan setjast saman til ein stav som er like lang som den svarte staven.
Gi elevane tid til å undersøkje sortering av storleikar og kva for brøkar dei forskjellige stavane representerer. Deretter kan dei dele og diskutere i plenum. La elevane eller gruppene forklare vala sine. Usemje mellom gruppene kan gi fruktbare diskusjonar. Oppfordre alle gruppene til å forklare korleis dei har resonnert.
Gode rettleiingsspørsmål
- Kvifor stemmer det du har valt?
- Kan du finne ein måte å skrive det ned på?
- Kvifor har du valt desse brøkane?
Mogleg utviding
Elevar eller grupper som blir fort ferdige, kan samanlikne kvar brøk med andre storleikar, for eksempel: «E er \(1\frac13\) av A, sida E = 32 og A = 24»
Mogleg støtte
Somme elevar kan trenge støtte for å forstå at staven med lengde 48 er \(1\frac23\). Det kan vere til hjelp å undersøkje kva \(1\frac23\) er som uekte brøk.
Ressursen er utviklet av NRICH