Maxikant
Aktivitet
Når de vil arbeide med dette problemet, kan du skrive ut kopioriginalen.
Alternativt kan du bruke dette interaktive tegnearket (ekstern side).
Teikn nokre mangekantar mellom punkta i eit 3 x 3-nett.
Kva er det største sidetalet ein mangekant i dette rutenettet kan ha?
Korleis blir det med eit 3 x 4-rutenett, eller eit 3 x 5-rutenett?
Og med eit 3 x n-rutenett?
Kan du forklare eit mønster som viser korleis sidetalet aukar?
Undersøk nokre rutenett som har fire prikkar i høgda.
Kva er største sidetalet i ein mangekant i eit 4 x n-rutenett?
Kan du forklare korleis du veit at du har funne det største moglege talet?
Kva er det største sidetalet i ein mangekant i eit 6 x 6-rutenett?
Og i eit 6 x n-rutenett?
Starthjelp
Vil systemet bli forskjellig, avhengig av om n er eit partal eller eit oddetal?
Løysing
I eit 3 x 3-rutenett har mangekanten høgst 7 sider.
I eit 3 x 4-rutenett har mangekanten høgst 10 sider, og i eit 3 x 5-rutenett har han høgst 13 sider.
I eit 3 x n-rutenett har mangekanten høgst 3 ∙ n – 2 sider (dvs. talet på prikkar minus 2).
Ei løysing kan for eksempel sjå slik ut:
Ei løysing med fire prikkar i høgda kan sjå slik ut:
Her er sidetalet lik 4n, det vil seie talet på prikkar.
Lærarrettleiing
Kvifor arbeida med denne oppgåva?
I denne aktiviteten møter elevane fleire ulike mangekantar, som ikkje nødvendigvis liknar dei tradisjonelle mangekantane elevane er van til å arbeide med. Aktiviteten bidreg til å utvide forståinga av mangekantar og korleis dei kan sjå ut. I tillegg legg aktiviteten til rette for utforsking av ulike moglegheiter, resonnering og generalisering.
Mogleg tilnærming
Teikn eit 3 x 3-rutenett på tavla. Be elevane om å foreslå korleis ein mangekant kan teiknast i rutenettet. Spør så om det største tal på sider ein mangekant i dette rutenettet kan ha.
Elevane kan arbeide i par og utforske oppgåva. Del ut kopioriginalen, eller la elevane bruke det interaktive teiknearket.
Når elevane har funne ei løysing, kan dei arbeide vidare med 3 x 4-rutenett og 3 x 5-rutenett. Ei moglegheit er å teikne opp dei ulike løysingane med flest kantar på tavla. Klarer nokon å finne ei løysing med fleire kantar?
Elevane kan så utforske og prøve å forklare eit mønster som viser korleis talet på sider aukar i eit 3 x n-rutenett. Klarer dei å lage ein regel?
Vidare kan dei utforske største talet på sider i ein mangekant i eit 4 x n-rutenett.
Til slutt samlar du klassen til ein diskusjon i plenum. Kva har de funne ut? Korleis veit de at de har funne det største moglege talet? Korleis aukar det moglege talet på sider i ein mangekant når rutenettet blir breiare?
Mogleg utviding
Kva er det største moglege talet sider i ein mangekant i eit 5 x 5-rutenett? Kva med eit 5 x n-rutenett?
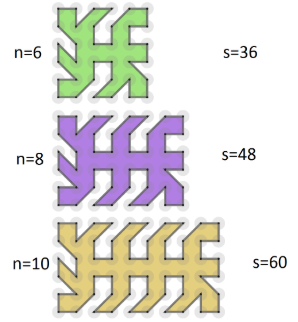
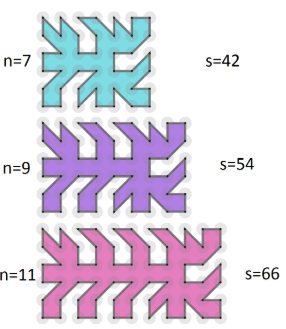
Her er nokre døme på løysingar i rutenett med 6 punkt i høgda.
Kva er det største moglege talet sider i ein mangekant i eit 6 x n-rutenett?
Send inn elevsvar
Ressursen er utviklet av NRICH