Brøkveggen
Aktivitet
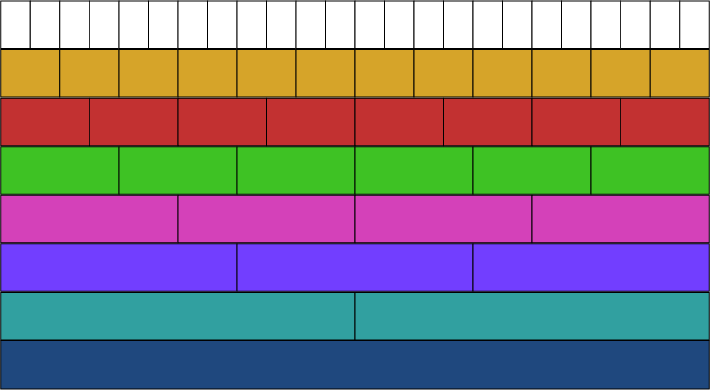
Studer bildet over. På hvor mange forskjellige måter kan du finne og skrive \(\frac12\)?
Hvilke likeverdige brøker for \(\frac13\) kan du finne?
Ved å bruke bildet av brøkveggen, hvordan kan du skrive \(\frac34\) på flere måter?
Nevn noen andre brøker som tilsvarer \(\frac12\).
Nevn noen andre brøker som tilsvarer \(\frac34\).
Kan du lage noen «regler» for å finne likeverdige brøker?
Du kan skrive ut en kopioriginal med bilde av brøkveggen.
Lærerveiledning
Hvorfor arbeide med denne oppgaven?
Oppgaven kan brukes som en introduksjon til ekvivalente (likeverdige) brøker. Denne visuelle representasjon vil hjelpe elevene med å utvikle en forståelse av forholdet mellom ulike brøker. Den gir dem mulighet til å utforske brøker på en enkel og åpen måte, og oppmuntrer dem til å utvikle egne «regler» for å finne likeverdige brøker.
Mulig tilnærming
Introduser aktiviteten ved å presentere brøkveggen for klassen. Spør elevene hva de ser, og be dem dele observasjonene sine med en medelev. Elevene deler deretter ideene i plenum. Læreren kan styre samtalen mot brøk dersom elevene ikke naturlig kommer inn på det. Still åpne spørsmål om brøkene som er representert av de ulike stavene i bildet, og bruk den lilla staven som «helhet». Oppdager elevene noen brøker som er likeverdige? Spørsmål som «Hvor mange kvarte er det samme som en halv?» kan oppmuntre barn til å sette stavene sammen for å lage brøker som tjuefiredeler, i stedet for å se bare på enhetsbrøkene representert av individuelle staver.
Gi elevene litt tid til å jobbe to og to for å finne ekvivalente brøker ved å bruke brøkveggen. En utskriftsvennlig versjon er tilgjengelig her: Word, PDF. Oppmuntre elevene til å notere ned brøkene, og observer hva de oppdager med tellerne og nevnerne til de ekvivalente brøkene. La elevene få dele oppdagelsene sine i plenum. Har noen funnet en «regel» for å finne ekvivalente brøker uten å bruke bildet? Hvorfor fungerer denne «regelen»?
Elevene bør ha tilgang til centikuber eller multilink-kuber når de jobber i par eller små grupper. Hver stople kan da ha lik farge hele tiden. De kan bruke dette arket (Word, PDF) sammen med litt kvadratisk papir til å lage papirkopier av hver stolpe. Det kan være nyttig for barn å lage flere versjoner av samme stav for å se at de kan monteres sammen til samme lengde som den svarte staven.
Gi elevene litt tid til å undersøke størrelsesrekkefølgen på stavene, og hvilken brøk hver stolpe representerer. De bør få mulighet til å dele og forklare ideene sine i plenum. Det kan oppstå uenigheter mellom grupper. Dette kan fremme en sunn diskusjon, der det er viktig å oppmuntre hver gruppe til å begrunne forslaget sitt.
Gode veiledningsspørsmål
- Hvilken brøkdel av den lilla staven representerer hver blå søyle? Hvordan vet du det?
- Hvor mange seksdeler er det samme som en tredel?
- Skriv ned de likeverdige brøkene som du har funnet. Hva legger du merke til?
Mulig støtte
Noen elever kan finne det nyttig å tegne linjer på brøkveggen eller klippe ut de forskjellige brøkene for å kontrollere at de er identiske. Å bruke cuisenairestaver til å representere brøkene (kanskje velge en stav med lengde 6 eller 8 for å representere helheten) kan være hensiktsmessig for elever i oppstarten.
Elevsvar
På denne oppgaven har vi fått et løsningsforslag fra Krishna som går på skole i Ahmedabad i India. Krishna skriver at brøker beskriver en delmengde og består av teller og nevner. Nevneren forteller oss hvor mange deler en hel er delt opp i, mens nevneren forteller oss hvor mange av disse delene vi har. Brøker kan skrives på formen \(\frac PQ\), hvor \(Q\ \neq 0\). Krishna mener brøkvegger er en av de beste representasjonene som kan brukes for å forstå brøkbegrepet.
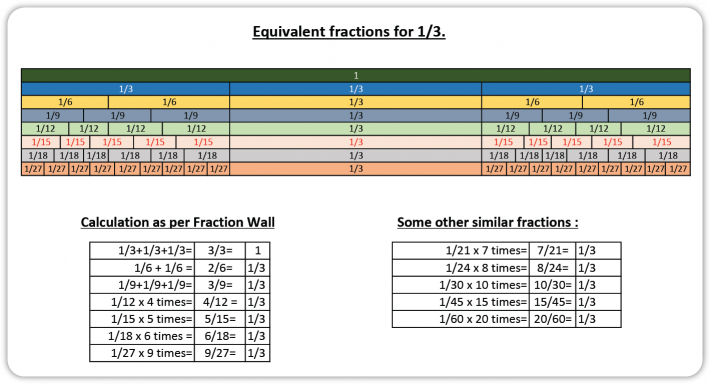
Krishna har også satt opp sine egne brøkvegger for å svare på spørsmålene i oppgaven, nedenfor kan du se inndelinger som alle gir \(\frac13\):
Krishna har også skrevet regler for hvordan vi kan finne like brøker, både ved forkorting og utviding (engelsk):
Tusen takk for gode løsningsforslag!
Ressursen er utviklet av NRICH