LAST NED kopioriginaler

Nedsenking

Stikkord: Volum Grafer Resonnering

Aktivitet

Fire legemer i gull

Anta at du har følgende kompakte geometriske legemer:

  1. En kule med radius lik 1 cm.
  2. En sylinder med høyde \(\frac43\) cm og radius 1 cm.
  3. En kjegle med radius 1 cm i grunnflaten og høyde 4 cm.
  4. En sylinder med høyde \(\frac49\) cm, gjennomboret på langs slik at snittflaten på sylinderen ser ut som en ring med indre radius 1 cm og ytre radius 2 cm.

Lag en skisse av hvert av legemene.

Kan du finne volumet av dem?

 

Et forsøk blir utført slik at det først festes et tynt snøre til de tredimensjonale legemene i et bestemt punkt. Deretter senkes hvert legeme ned i et målebeger med vann med en hastighet på 1 cm per minutt. Samtidig måles volumet av det fortrengte vannet, og det lages en graf for det i forhold til tiden som har gått.

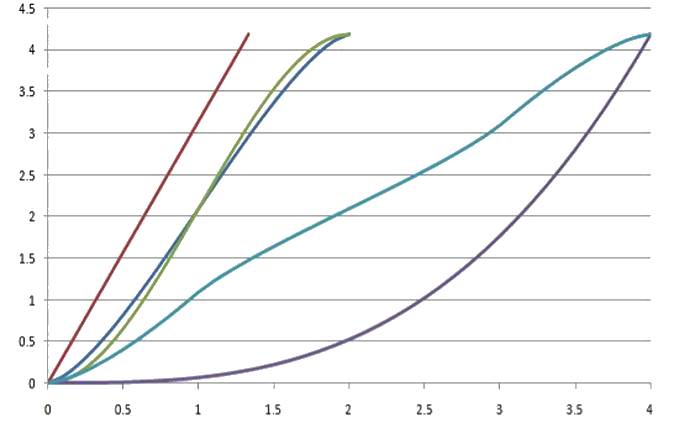
Resultatene ser du i dette diagrammet:

Diagram

Kan du finne ut hva de to aksene representerer?

Finn ut hvilken graf som korresponderer med de ulike legemene, og på hvilken måte de senkes ned i vannet. (Merk: Et av legemene brukes to ganger og senkes ned på to forskjellige måter.)

Tegn en skisse av grafene for de samme legemene dersom de senkes ned på andre måter.

Starthjelp

  • Alle legemene vil til slutt fortrenge samme volum væske.
  • Hva er nøkkelegenskapene hos hvert legeme? Hva vil skje med grafen når legemene senkes ned? Kan du finne igjen nøkkelegenskapene på grafen?
  • Det er ikke nødvendig å bruke mye algebra for å finne ut hvilken graf som hører til hvilket legeme!

Lærerveiledning

Hvorfor arbeide med denne oppgaven?

Oppgaven gir elevene mulighet til å tolke hvordan grafen utvikler seg, og deretter koble grafen til de ulike legemene. De må resonnere for å finne ut hvilken graf som hører til hvilket legeme, og de må forklare ideene sine. Underveis får de sjansen til å repetere formlene for volumet av tredimensjonale figurer.

Mulig tilnærming

Begynn med å be elevene tegne de fire figurene i oppgaven:

  1. En kule med radius lik 1 cm.
  2. En sylinder med høyde \(\frac43\) cm og radius 1 cm.
  3. En kjegle med radius 1 cm i grunnflaten og høyde 4 cm.
  4. En sylinder med høyde \(\frac49\) cm, gjennomboret på langs slik at snittflaten på sylinderen ser ut som en ring med indre radius 1 cm og ytre radius 2 cm.

Deretter kan elevene finne volumet for hvert legeme. Det gir også en god mulighet til å diskutere fordelene med å uttrykke svaret med π.

Del så ut arbeidsarket (lenke) med de fem grafene. Utfordre elevene til å navngi aksene og de fem grafene. La dem markere nøkkelpunkter langs grafene, og notere hva som skjer der, og hvorfor/hvordan de henger sammen med legemene.

Til slutt kan klassen samles til en diskusjon der elevene drøfter hverandres svar, og hvordan de fant ut hvilken graf som hører til hvilket legeme.

Gode veiledningsspørsmål

  • Hvilke egenskaper må legemet som hører til den lineære grafen, ha?
  • Hvilken av grafene har et økende stigningstall? Hvilke egenskaper kan denne figuren ha?
  • Finnes det noen symmetriske egenskaper hos legemene som kan knytte dem til den korrekte grafen?

Mulig utvidelse

Utforsk andre tredimensjonale geometriske figurer, for eksempel kube, pyramide eller ulike prismer. Hvordan vil grafene til disse figurene se ut ved nedsenking?

Ressursen er utviklet av NRICH

9,10