Speiling av rette linjer
Aktivitet
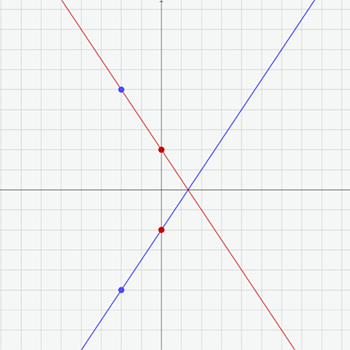
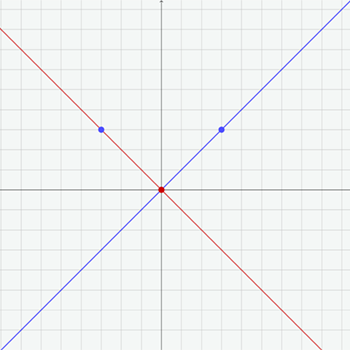
Her er det to sett med grafer. Hvert sett viser to linjer som er speilbilder av hverandre. Den ene grafen viser speiling om den horisontale aksen, og den andre viser speiling om den vertikale aksen.
Beveg de røde og blå punktene på det interaktive området nedenfor, og lag flere par rette linjer som er speilbilder av hverandre.
Hva kan du si om likningene til to linjer, der den ene er et speilbilde av den andre om den horisontale aksen?
Og hva kan du si hvis den andre er et speilbilde om den vertikale aksen?
Nedenfor ser du likningene til 16 rette linjer. Hver linje har en partner, enten som et speilbilde om den vertikale aksen eller som et speilbilde om den horisontale aksen.
Se på likningene uten å tegne grafer. Forsøk å finne ut hvilke par som hører sammen, og hvilke akser de er speilet om.
| \(y=3x+\frac14\) | \(y=4x+3\) | \(y=2x+4\) | \(y=2x+\frac14\) |
| \(y=-\frac14x+3\) | \(y=-4x-2\) | \(y=\frac14x+2\) | \(y=-2x-4\) |
| \(y=-\frac14x+2\) | \(y=3x+4\) | \(y=-3x-\frac14\) | \(y=\frac14x-3\) |
| \(y=-2x+\frac14\) | \(y=-4x+3\) | \(y=4x+2\) | \(y=-3x+4\) |
Anta at en linje er speilet om en akse, og at dette speilbildet igjen er speilet om den andre aksen.
Går det an å si noe om likningen til den siste linjen hvis du kjenner uttrykket for den opprinnelige linjen?
Har det noe å si hvilken akse du begynner speilingen med?
Forklar hvordan du resonnerer, og hva du kommer fram til.
Starthjelp
Begynn med å undersøke noen likninger som det er lett å tegne grafen til.
Lærerveiledning
Hvorfor arbeide med denne oppgaven?
Oppgaven hjelper elevene til å sikre forståelsen av hvordan likninger på formen y = ax + b beskriver stigningsforhold og plassering av en linje i et koordinatsystem. Elevene utforsker hvordan en speiling av linjen vil påvirke likningen til linjen. De blir oppmuntret til å visualisere hvordan grafene beveger seg, for å få bekreftet om antakelsene deres stemmer eller ikke.
Oppgaven er fin med tanke på videre arbeid med å omforme grafene til mer kompliserte funksjoner.
Mulig tilnærming
Det er nyttig hvis elevene har gjort noe innledende arbeid med å tegne grafen til rette linjer.
Denne oppgaven passer godt sammen med oppgaven Utforsk rette linjer (aktiveres). Den inneholder en interaktiv del som det kan være lurt å la hele klassen arbeide med samtidig.
Ta utgangspunkt i posisjonen til en av linjene. Be klassen beskrive hvordan de vil speile linjen om hver av aksene.
Hvordan kan de være sikre på at det de har gjort, er korrekt?
Gi elevene god tid, gjerne ved at de jobber to og to på en PC, slik at de kan oppdage hvilken effekt speilingene har på likningene til linjene.
Gjør det tydelig overfor elevene at målet må være at de skal kunne foreslå et uttrykk for den nye likningen, så snart en linje er speilet om en av aksene.
Samle klassen etter en stund, og benytt den interaktive delen til å se om elevene har evne til dette.
Gjør det samme med forskjellige linjer og speilinger om begge aksene, helt til elevene føler seg trygge nok til å foreslå nye likninger.
La elevene dele kunnskapen sin og forklaringene og begrunnelsene sine.
Del ut aktivitetskortet for å kontrollere at elevene kan sette sammen par som er speilbilder av hverandre, og identifisere symmetrilinjen.
Hvis elevene trenger lengre tid til å bli trygge, kan de lage egne kort og utfordre medelever til å finne likninger som hører sammen.
Introduser elevene for den siste delen av oppgaven: Kan de forutsi uttrykket for linjen de får når den opprinnelige linjen speiles om en akse, før dette speilbildet igjen speiles om den andre aksen?
La elevene forklare og begrunne det de har funnet ut, enten ved at de lager en plakat som de viser fram, eller ved at de lager en presentasjon for hele klassen.
Gode veiledningsspørsmål
- Hva blir forandret når vi speiler grafen til en rett linje? Og hva forblir det samme?
- Hvordan påvirker dette likningen til grafen?
- Hva blir effekten av speiling om to akser, og hvordan blir det hvis vi bytter om på rekkefølgen?
Mulig utvidelse
Velg en rett linje som ikke går gjennom origo. Speil denne linjen om en av aksene.
Nå har du to linjer, og disse to skal du speile om den andre aksen.
Hvilken figur er dannet av disse fire linjene? Og hva er arealet av figuren?
Finn en måte å forutsi arealet på bare ut fra likningen til den første linjen, uten å tegne noen grafer.
Mulig støtte
Forsikre deg om at elevene er trygge på sammenhengen mellom egenskapene til en rett linje og likningen til linjen.
Oppmuntre elevene til å tegne grafen til flere rette linjer, og bruk det interaktive området til å teste ut forslagene deres.
Ressursen er utviklet av NRICH