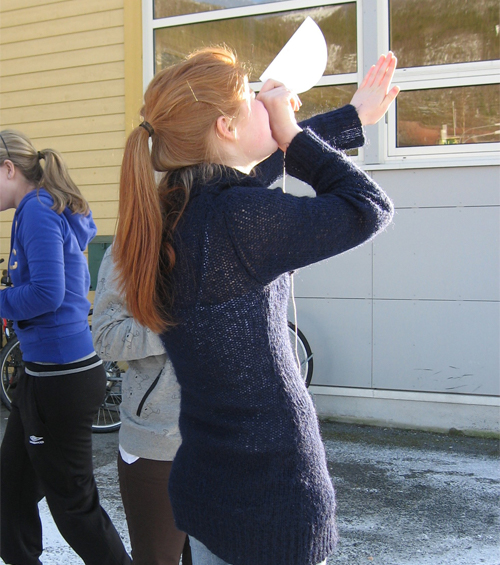Hvor høy er flaggstanga?
Aktivitet
Denne oppgaven kan dere gjøre når dere har lært definisjonene av forholdene sinus, cosinus og tangens til vinkler i rettvinklede trekanter, og dere kan finne disse verdiene ved hjelp av en kalkulator.
I denne aktiviteten må to og to samarbeide.
Dere trenger ei sikteskive, et langt målebånd, skrivesaker og ei gradskive.
- Først må dere lage sikteskiva:
Dere trenger et stykke litt stiv papp med (minst) ei helt rett side på 15-20 cm, og ca. 50 cm. tynn hyssing.
Tegn en rett linje ca \(\frac12\:cm\) innenfor den rette kanten på pappstykket. Lag et hull i pappskiva et sted på denne linja, og tre hyssingen gjennom. Knyt en knute i den ene enden, slik at den ikke glir gjennom hullet. Knyt for eksempel et viskelær, en blyant eller en binders i den andre enden av hyssingen, slik bildet viser. - Dere skal gå ut og ved hjelp av enkle målinger få nok informasjon til å regne ut høyden på et hus eller en flaggstang eller noe dere selv velger. Dere må kunne se toppen på det dere skal finne høyden av. Og det må være mulig å måle avstanden på bakken fra rett under det dere har valgt å finne høyden av, til det punktet hvor dere står.
Dere skal velge to punkt hvor dere skal stå og utføre målingene, la det være ca 5 meter mellom de to punktene.
- Dere skal måle avstanden fra punktet hvor dere står til punktet loddrett under det dere skal finne høyden av. Noter!
- Den ene av dere skal sikte langs den rette siden av sikteskiva rett mot toppen av flaggstanga elle husmønet eller det punktet dere har valgt. Den andre skal lage et tydelig merke på pappskive der hyssingen (loddsnora) henger.
- Gjenta punkt a og b med en annen avstand. Pass på å markere hvilken vinkel som hører til hver måling.
Nå har dere to sett med opplysninger, en avstand og en vinkel til hver måling.
Hvor høy er flaggstanga, eller huset eller det dere skal finne høyden av?
Starthjelp
- Kan dere tegne hjelpefigurer til de to situasjonene?
- Kan dere sette mål på figurene?
- Hvilken størrelse på hjelpefiguren skal dere finne?
Løsning
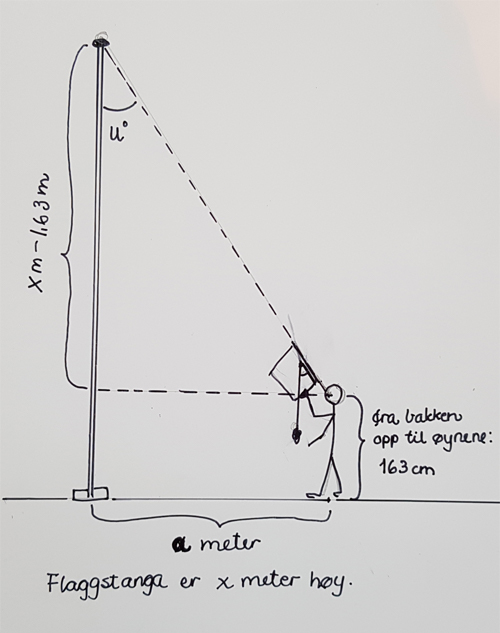
I løsningsforslaget tenker vi oss at klassen skulle finne høyden av ei flaggstang. Hjelpefiguren kan for eksempel se slik ut:
Vi må huske at målingen starter ved øynene til den som står med sikteskiva, så man må finne og ta hensyn til denne høydeb. Og vi må være oppmerksomme på at vinkelen som blir markert på sikteskiva er den samme som vinkelen mellom flaggstanga og siktelinja.
Hvis vi kaller denne vinkelen u, vet vi at \(\tan u=\frac{a}{x-1,63}\). Når vi setter inn tall for u og a, får vi likningen
\(x-1,63=\frac{a}{\tan u}\\ x=\frac{a}{\tan u}+1,63 \)
Dette blir høyden til flaggstanga i meter.
Lærerveiledning
Hvorfor arbeide med denne oppgaven?
Elevene som gjør denne oppgaven har lært om sinus, cosinus og tangens til vinkler i rettvinklede trekanter. De har funnet disse forholdene når (minst) to av sidene i en rettvinklet trekant er kjent, de har funnet disse verdiene på kalkulatoren og brukt dem til å beregne sider i rettvinklede trekanter, og de har funnet vinkler når de kjenner en sinus, cosinus eller tangensverdi.
Hvis de hadde fått denne oppgaven ferdig skissert med hjelpefigur og alle opplysninger markert, ville dett bare vært en ny oppgave av samme sort som de allerede har løst mange av. Nå gjør vi oppgaven mer åpen og lar elevene selv få ansvar for å finne en framgangsmåte og en løsning.
Mulig tilnærming
Elevene må arbeide i par. De må få utstyr til å lage sikteskivene, - papp med en rett kant, hyssing og gradskive. Og de må få veiledning i hvordan de lager den. (Eller om du vil: Du kan lage skivene klar til elevene på forhånd.) Du bør på forhånd ha funnet noe som elevene skal finne høyden av, så nær skolen at de ikke bruker mye tid på å komme fram til arbeidsstedet ute.
Forklar elevene hva oppgaven går ut på:
«Dere skal velge to punkt hvor dere skal stå og utføre målingene, la det være ca. 5 meter mellom de to punktene.
- Dere skal måle avstanden fra punktet hvor dere står til punktet loddrett under det dere skal finne høyden av. Noter!
- Den ene av dere skal sikte langs den rette siden av sikteskiva rett mot toppen av flaggstanga eller husmønet eller det punktet dere har valgt. Den andre skal lage et tydelig merke på pappskiva der hyssingen (loddsnora) henger.
- Gjenta punkt a og b med en annen avstand. Pass på å markere hvilken vinkel som hører til hver måling.»
Når disse beskjedene er gitt, skal elevene få arbeide på egen hånd. Følg med på arbeidet, men unngå å korrigere eller veilede. De eneste rådene de kan få, er at det kan være nyttig med en hjelpefigur for hver av de to situasjonene, og at de må skrive målene på figurene.
I løpet av arbeidet vil elevene helt sikkert sammenligne løsningene sine. De kommer antakelig til å få ulike svar, og diskusjonene mellom arbeidsparene kan være nyttige. De kan lytte til hverandres resonnement og vurdere, hvis to par har resonnert forskjellig, hva kan være riktig? Kanskje noen vil ut igjen for å måle på nytt. Kanskje noen vil gjøre utregningen på nytt. La elevene få god tid til å fullføre arbeidet.
Til slutt må løsningene presenteres. Hvis du har sett noen med ufullstendige, tungvinte eller gale løsninger, må disse også få slippe til. Det er mye å lære av å vurdere hverandres resonnement. Det må være aksept i klassen for at det er nyttig å få fram feilsvar slik at de kan rettes, og misforståelser kan ryddes av veien. Til slutt må dere bli enige om hva som er rett: Hvordan er det mest effektivt å løse oppgaven? Og hvor høyt var det de skulle måle, - egentlig?
Gode veiledningsspørsmål
- Kan dere tegne hjelpefigurer til de to situasjonene?
- Kan dere sette mål på figurene?
- Hvilken størrelse på hjelpefiguren skal dere finne?
Mulig støtte
Et lite tips: Kanskje neste prøve, med trigonometri som tema, kan inneholde en oppgave om noen som skal måle høyden av ei flaggstang ved å måle avstanden til flaggstanga og en vinkel ved hjelp av sikteskive?
Send inn elevsvar
Ressursen er utviklet av Matematikksenteret