Datamatching
Aktivitet
I Matteby har det vært fire bankran på samme kveld!
I hver bank har ranerne kommet seg inn ved å bruke en inngangskode på fire bokstaver, der bokstavene står i omvendt alfabetisk rekkefølge.
En kriminell bande med 16 personer er mistenkt, men det er vanskelig å bevise at det er de som har utført ranene.
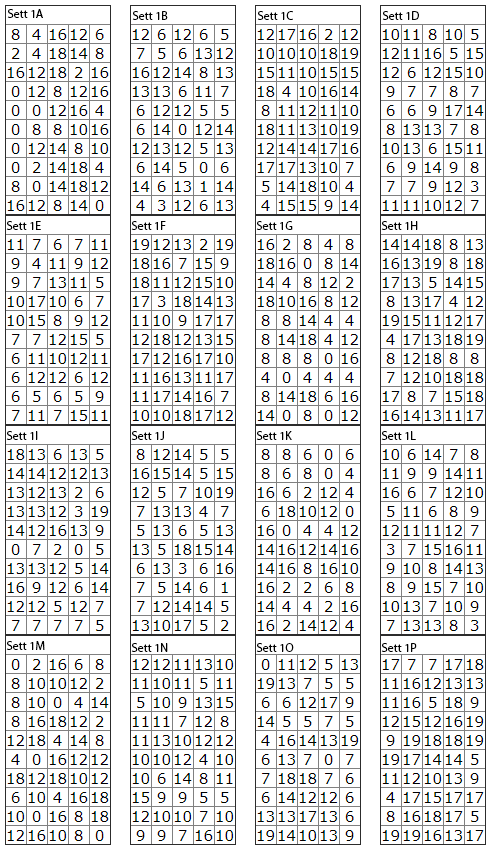
Detektiv Matteson var med å ransakte banden, og de fant 1 lapp med noen koder i lomma til hver av personene. Det ser ut til å være datasett med navn fra A til P.
Detektiv Matteson tror at disse datasettene inneholder inngangskodene til bankene, og at ranerne hadde delt seg i fire ulike grupper som ranet hver sin bank. Hvis han kan finne ut av hvilke sett som hører sammen så kan han bevise at ranerne hadde riktig kombinasjon av bokstaver for å komme seg inn i hver bank.
Kan du hjelpe detektiv Matteson med å sortere datasettene i fire grupper der dataene i hver gruppe har de samme hovedtrekkene?
Hva var inngangskoden til hver av de fire bankene?
Du kan finne dataene i dette regnearket i GeoGebra.
Eller du kan finne listene i dette regnearket (Excel).
Starthjelp
- Det kan være en god idé å regne ut gjennomsnitt og spredningsmål (f.eks. standardavvik) for hver liste.
- Du kan også tegne søylediagram eller histogram for hver liste og sammenligne.
Løsning
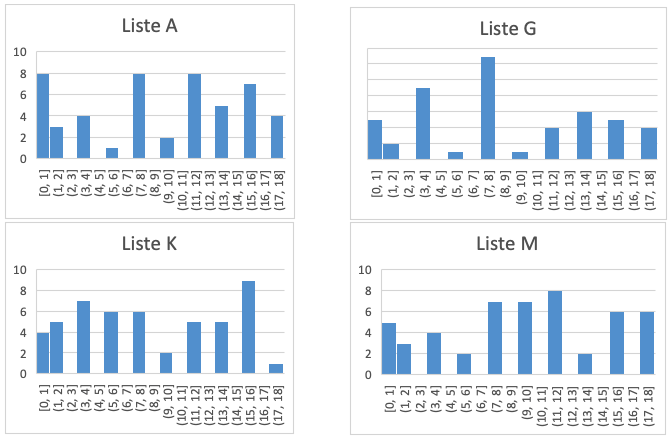
På figurene har vi tegnet histogram og valgt søylebredde 1.
Vær oppmerksom på at de ikke har identiske fordelinger! Vi ser etter hovedtrekkene i fordelingene, og sorterer dem i grupper etter det.
1. Listene A, G, K og M har ingen oddetall, så disse listene kan samles i en gruppe.
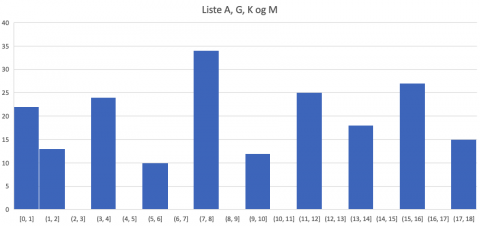
Om vi setter dataene fra de fire listene i samme histogram, blir det seende slik ut:
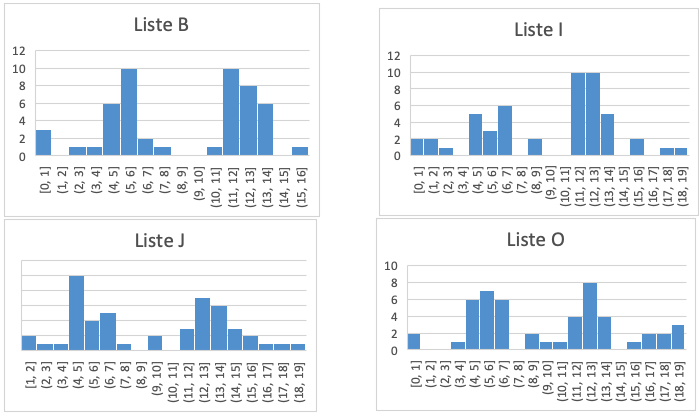
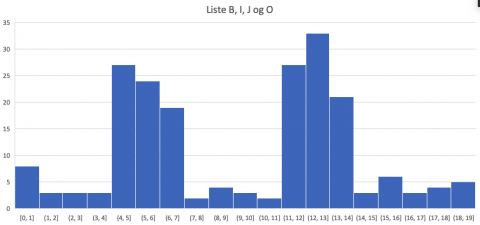
2. Listene B, I, J og O har nesten alle tallene samlet rundt 6-7 og 12-13. De har to "topper", så disse fire listene hører til samme gruppe.
Om vi setter dataene fra de fire listene i samme histogram, blir det seende slik ut:
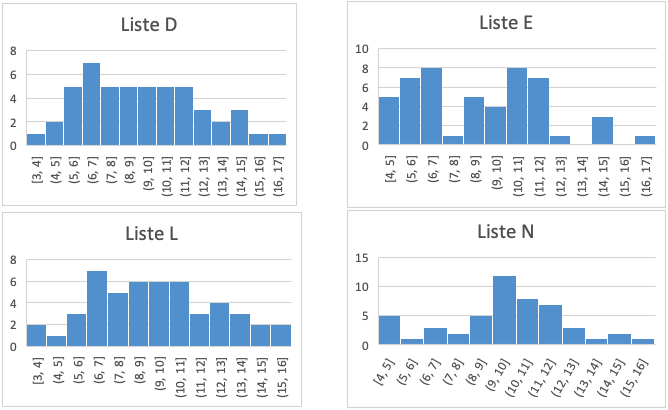
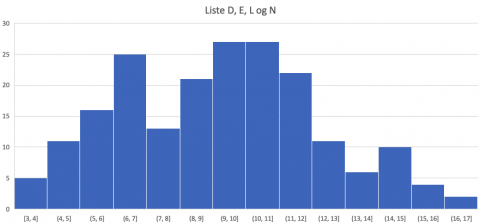
3. Listene D, E, L og N har bare noen få store og små tall. De fleste tallene er gruppert rundt midten, så disse fire kan settes i en gruppe.
Om vi setter dataene fra de fire listene i samme histogram, blir det seende slik ut:
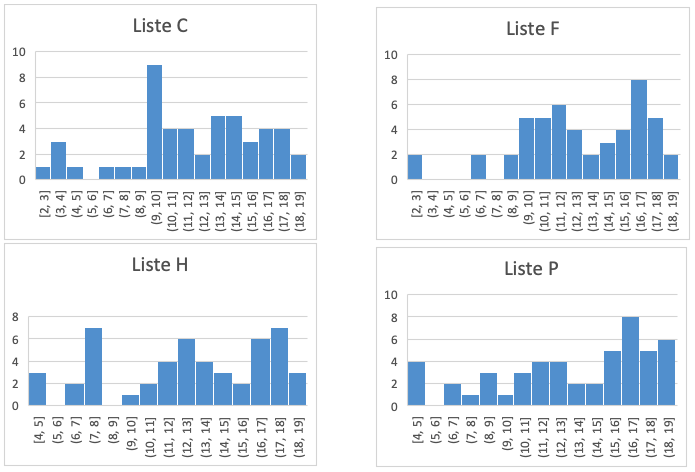
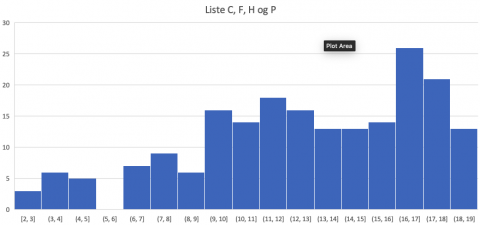
4. Listene C, F, H og P har lignende hovedtrekk. Tallene stiger opp til 17, og etter 17 faller de bratt ned (på grafen). Tyngdepunktet er litt mer til høyre enn i de fire foregående histogrammene.
Om vi setter dataene fra de fire listene i samme histogram, blir det seende slik ut:
Vi kan bruke regnearket til å finne gjennomsnitt og standardavvik for alle listene:
Vi lar regnearket runde av alle verdiene til hele tall og se om det da er lettere å finne mønster:
Her skiller listene C, F, H og P seg ut ved at de har høyere gjennomsnittsverdier enn de andre. Det svarer til at grafene har tyngdepunkt lenger til høyre på disse fire grafene enn på de andre.
Det er fire lister som får standardavvik 6 – A, G, K og M, og alle de andre har mindre standardavvik. Dette er den gruppa som inneholder bare partall.
Det er fire lister som får standardavvik 3, og alle de andre har større standardavvik. Det gjelder listene D, E, L og N. Alle disse listene hadde grafer med størst samling av data rundt midten.
Lærerveiledning
Hvorfor arbeide med denne oppgaven?
Med oppgaven ønsker vi å trigge elevenes nysgjerrighet og hjelpe dem til å se hvor viktig det er å kunne løse «omvendte» problemer, som her i oppgaven der de får lister med data, og utfordringen er å lete etter de underliggende strukturene.
Oppgaven illustrerer konseptet med sannsynlighetsfordeling: Ulike utfall er mulig, og hvert utfall forekommer med en viss frekvens. Oppgaven vil hjelpe elevene til å forstå at selv om resultatet av hvert forsøk i en tilfeldig forsøksserie er uforutsigbart, vil en stor mengde data ha forutsigbare mønster.
Mulig tilnærming
Når eleven skal arbeide med denne oppgaven, bør de ha mulighet til å gjøre det digitalt. De må få tilgang til filene med data, enten med denne Excel-fila, eller denne GeoGebra-fila.
Be elevene arbeide parvis med datasettene, skrive ned det de legger merke til, og bruke regnearkene til å tegne grafer eller regne ut statistiske verdier (som gjennomsnitt og standardavvik).
Så snart de mener at de har sortert listene i fire grupper etter felles egenskaper, kan klassen samles til en samtale om løsningene. Legg vekt på at elevene forklarer tydelig hvorfor de har gruppert som de har gjort. Er de andre enige? Har noen løst oppgaven annerledes? Kan elevene hjelpe hverandre til å forbedre og gjøre argumentasjonen klarere?
Gode veiledningsspørsmål
- Beskriv hver liste med ord: Hva ser ut til å være karakteristisk?
- Hvordan vil du arbeide for å gjøre beskrivelsen av hver liste mer presis? Hvordan kan du representere hver av gruppene med data?
- Kan du se noen mønster som finnes i flere av listene? Kan det hjelpe deg i gang med å gruppere listene med data?
- Kan du tegne noen diagram eller grafer som representerer fordelingen i datasettene?
Mulig utvidelse
Så snart listene er sortert i fire grupper, kan elevene foreslå hvilke sannsynlighetsfordelinger som beskriver fordelingene.
Mulig støtte
I aktiviteten «Hvilke lister hører sammen?» introduseres et lignende problem med seks lister som hører til to ulike grupper datasett. Det kan være enklere for elevene å begynne med det.
Ressursen er utviklet av NRICH