Ikke-transitive terninger
Aktivitet
Her ser du tre terninger som brukes til å spille et spill for to personer.
- Den grønne terningen har tallene {2, 2, 4, 4, 9, 9}.
- Den røde terningen har tallene {1, 1, 6, 6, 8, 8}.
- Den blå terningen har tallene {3, 3, 5, 5, 7, 7}.
Hver spiller velger en terning.
Spillerne triller terningene sine.
Vinneren er den personen som får det største tallet.
Karl og Alise spiller spillet. Karl vil være førstemann, så Alise lar han få lov til det.
Var det så lurt?
Kan du gi et tips til hvilken terning Alise bør velge, når hun vet hvilken terning Karl har valgt?
Starthjelp
- Hva bør Alise velge dersom Karl velger den grønne terningen?
- Hva bør Alise velge dersom Karl velger den røde terningen?
- Hva bør Alise velge dersom Karl velger den blå terningen?
Løsning
Om Karl velger den røde terningen, er det lurt av Alise å velge den grønne terningen, siden den har to tall som er større enn de som er på den røde. Om Karl velger den grønne, er det lurt av Alise å velge den blå, siden den har to tall som er større en n de på den grønne. Om Karl velger den blå, er det lurt av Alise å velge den røde, siden den har to tall som er større enn de på den blå.
De tre ikke-transitive terningene er laget slik at alle slår én terning, og alle taper mot én terning. Dette er det samme prinsippet som når en spiller «stein, saks, papir».
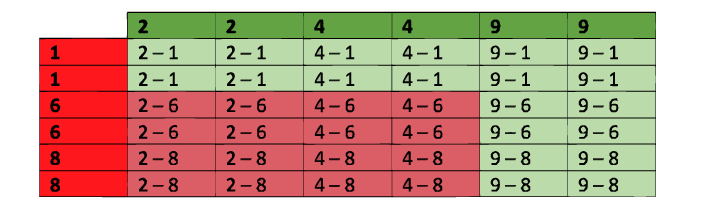
Tabellen viser utfallsrommet når grønn terning blir kastet mot rød terning. Vi ser at det er 36 mulige utfall. I 20 av dem vinner grønn, i 16 vinner rød. Sannsynligheten for grønn seier er da \(\frac{20}{36}=\frac59\), mens sannsynligheten for rød seier er \(\frac{16}{36}=\frac49\). Det vil altså være lurt å velge grønn terning dersom motspilleren har valgt rød.
Lærerveiledning
Hvorfor arbeide med denne oppgaven?
Denne oppgaven legger til rette for introduksjon av eller øving med forskjellige diagramtyper. Transitivitet er et så vanlig fenomen at de fleste tar det for gitt. Elevene kan derfor bli forundret og nysgjerrige på ikke-transitive terninger.
Mulig tilnærming
Før du introduserer aktiviteten, bør du ha laget de tre terningene fra oppgaven.
«Vi skal spille et spill. Jeg trenger en frivillig til å velge en av disse tre terningene. Deretter skal jeg velge en terning, og så triller vi dem samtidig. Den med flest øyne på terningen vinner.» Vis elevene hvordan terningene ser ut, og hvor mange øyne det er på hver side.
Når den frivillige har valgt terning, velger du den som passer fra de to gjenværende (rød slår blå, blå slår grønn, og grønn slår rød). Trill terningene såpass mange ganger at elevene begynner å tvile på om det er et rettferdig spill. «Det ser ut som jeg er heldig i dag, eller så er kanskje terningen min sterkere enn din!»
«Vi skal spille spillet igjen på slutten av timen /om en stund. Jeg vil at dere skal utforske egenskapene til disse terningene, og gjøre dere opp en mening om dere tror spillet er rettferdig eller ikke. Dere skal også utvikle en strategi som er slik at dere kan velge den terningen som gir størst sannsynlighet for seier.»
Gå rundt og observer hvilke metoder elevene bruker når de arbeider med oppgaven i små grupper. Om noen har problemer med å komme i gang, kan du stille slike spørsmål:
- Hvilke utfall er mulig når rød spiller mot grønn? Hva med rød mot blå, eller grønn mot blå?
- Hvordan kan dere organisere informasjonen på en systematisk måte?
- Finnes det noen typer diagram som dere kan bruke, og som kan være til hjelp?
- Hvordan kan dere beregne sannsynligheten for hvert utfall?
Ta en pause etter en stund, slik at elevene kan dele og diskutere metoder i plenum. Om det er hensiktsmessig, kan du introdusere forskjellige diagrammer for å vise utfallsrommene i de forskjellige tilfellene. Deretter kan du gi elevene mer tid til å bruke de forskjellige metodene til å fullføre oppgaven.
Elever som blir tidlig ferdig, kan utfordres til å finne andre ikke-transitive terninger.
Til slutt samler du klassen og lar dem utfordre deg til et nytt spill der de bruker strategiene sine. Be dem forklare hvordan de kom fram til strategiene sine.
Ressursen er utviklet av NRICH