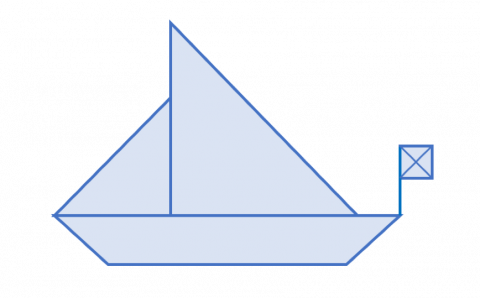
Puslespill seilbåt
Aktivitet
Her ser du biter som sammen blir en seilbåt. Tegn bitene på et ruteark (du kan skrive ut kopioriginalen Seilbåten og bruke bitene på side 2), klipp ut bitene og sett dem sammen til seilbåten. Du kan gjerne lime bitene på et annet ark.
Nå skal du forstørre seilbåten. Sidekanten som har lengde 4, skal få lengde 6. Forstørr alle bitene på tilsvarende måte, med samme forhold, og tegn de nye bitene på et ruteark eller på side 3 i kopioriginalen. Klipp ut bitene du har laget, og lag seilbåten. Den kan også limes på et ark.
Skriv ned det matematiske arbeidet du har gjort. Du kan skrive på et ark eller i boka di.
- Er den nye seilbåten lik den opprinnelige? Forklar og begrunn.
- Dersom båtene ikke har samme form, hva kan årsaken være?
- Hvordan tenkte du da du lagde bitene til den nye seilbåten?
Gjenta prosessen, men nå skal sidekanten som hadde lengde 4, få lengde 8. De andre bitene skal forstørres med samme forhold.
Skriv ned det matematiske arbeidet du har gjort. Du kan skrive på et ark eller i boka di.
- Er den nye seilbåten lik den opprinnelige? Forklar og begrunn.
- Dersom båtene ikke har samme form, hva kan årsaken være?
- Hvordan tenkte du da du lagde bitene til den nye seilbåten?
Aktiviteten er hentet fra Kartlegging av matematikkforståelse. Introduksjon til diagnostisk undervisning i matematikk (Brekke, 2002).
Løsning
1. Forholdet mellom den opprinnelige figuren og den nye forstørrende figuren blir \(6 \over 4\). Altså må alle sider multipliseres med \(6\over 4\) eller \(1,5\).
- Stor trekant: 9 ruter, 9 ruter og 9 «rute-diagonaler»
- Liten trekant: 6 ruter, 6 ruter og 6 «rute-diagonaler»
- Trapes: 12 ruter, 18 ruter, 3 «rute-diagonaler» og 3 «rute-diagonaler»
- Flaggstang: 3 ruter
- Kvadrat: 1,5 ruter
2. Forholdet mellom den opprinnelige figuren og den nye forstørrende figuren blir \(8 \over 4\). Altså må alle sider multipliseres med \(8 \over 4\) eller 2.
- Stor trekant: 12 ruter, 12 ruter og 12 «rute-diagonaler»
- Liten trekant: 8 ruter, 8 ruter og 8 «rute-diagonaler»
- Trapes: 16 ruter, 24 ruter, 4 «rute-diagonaler» og 4 «rute-diagonaler»
- Flaggstang: 4 ruter
- Kvadrat: 2 ruter
Lærerveiledning
Hvorfor arbeide med denne oppgaven?
Ved å arbeide med denne aktiviteten skal elevene finne og uttrykke sammenhengen mellom tallstørrelser, og se at de kan bruke brøk til å beskrive forholdet mellom ulike sider i en figur.
Aktiviteten gir mulighet til å observere om elevene identifiserer en multiplikativ sammenheng. Elever som tenker additivt i denne oppgaven (adderer 2 til alle lengdene), vil se at det nye puslespillet får en annen form enn utgangspunktet. Misoppfatningen kommer til syne, slik at de kan diskutere eller reflektere omkring den. Oppgaven er et eksempel på en aktivitet som kan skape en kognitiv konflikt.
Mulig tilnærming
Oppgaven kan introduseres både skriftlig og muntlig. Det vil være en fordel om elevene får arbeide med kopioriginalen Seilbåten, eller på et ruteark. De kan arbeide i par.
Ulike elevløsninger bør diskuteres i en matematisk samtale. Her kan det være lurt å løfte frem løsninger som tar utgangspunkt i den multiplikative sammenhengen mellom figurene og løsningsforslag som bygger på additiv tenkning. Da kan det skapes rom for å diskutere hva som skjer når seilbåten blir en større versjon av den de begynte med, og hva som skjer når den nye seilbåten ikke ligner utgangspunktet. Noen elever tror at forstørring betyr å lage hver bit større, uten å ha skjønt den matematiske ideen knyttet til forstørring, nemlig at formen skal være den samme etter forstørringen. Målet må være at elevene forstår at dette ikke skjer ved å addere en fast størrelse til alle målene.
Den neste aktiviteten, hvor sidene utvides fra 4 cm til 8 cm, er enklere, da de fleste vil ta i bruk strategien dobling. Disse to aktivitetene til sammen legger til rette for en god diskusjon med fokus på misoppfatninger og de multiplikative strukturene som opprettholder forholdene. Etter at elevene har møtt på en kognitiv konflikt, må de få støtte og veiledning slik at de kommer ut av konflikten.
Gode veiledningsspørsmål
Det er fint om elevene får streve litt med dette arbeidet før de veiledes videre. Veiledningen bør være resonnerende og gjerne rettet mot eventuelle kognitive konflikter som kan oppstå.
- Hvordan kan dere begynne, og hvorfor?
- Kan dere lage en visuell representasjon (for eksempel en tegning) som kan hjelpe dere til å løse oppgaven?
- Hvordan beholder dere en god oversikt over det dere har funnet ut?
- Hvilket regnestykke passer til situasjonen? Hva forteller regnestykket?
- Hvor mye lengre er sidelengden i den nye figuren i forhold til den første?
- Hva vil skje om alle lengdene blir to ruter lengre? Hva skjer med flagget?
Mulig utvidelse
Hvordan blir seilbåten om sidelengden som hadde 4 i lengde, nå skal få en lengde på 2 cm? Hva om den nye lengden blir 3 cm?
Gjennomfør aktiviteten med Puslespillet fly (se kopioriginal) etter samme oppskrift som for seilbåten.
Mulig støtte
Elever som strever med å se forskjellen på multiplikativ og additiv tenkning i arbeid med denne oppgaven, bør lage en båt hvor de legger til to ruter på alle lengdene, og en båt hvor de multipliserer alle lengdene med 2. Videre kan de studerer de ulike delene i de to båtene og se og sette ord på hva som skjer med formen på delene når de adderer, og hva som skjer når de multipliserer.