Symmetriproblemer
Aktivitet
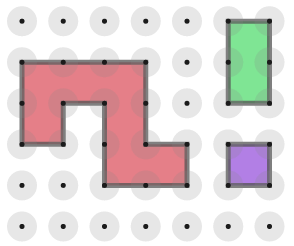
De tre delene på bildet under kan settes sammen slik at du får en form med minst én symmetrilinje. Hjørnene til alle delene må ligge i punkt i rutenettet, og ingen av delene må overlappe hverandre.
De tre delene må ligge inntil hverandre. På figuren nedenfor ligger den røde og den grønne biten inntil hverandre, men det er ikke lov å plassere den lilla på denne måten:
Løsningen nedenfor tilfredsstiller ikke kriteriene fordi den ikke har noen symmetrilinjer.
Kan du finne alle mulige måter å sette sammen bitene på slik at formen får minst én symmetrilinje? (Det finnes mer enn seks løsninger.)
Hvordan kan du forsikre deg om at du har funnet alle?
Her er noen flere problemer du kan utforske:
- Design dine egne tre figurer. La dem ha et totalt areal på 10 kvadratenheter, slik som figurene ovenfor. Hvor mange måter kan du kombinere dem på slik at du får symmetriske figurer?
- Kan du lage tre enkeltfigurer som kan settes sammen til flere symmetriske figurer enn de du kunne lage i oppgaven vi begynte med?
- Kan du lage tre enkeltfigurer som aldri kan settes sammen til noen symmetrisk figur?
Du kan skrive ut et bilde av de tre figurene i oppgaven for å klippe dem ut her.
I appleten nedenfor kan du prøve ut ideene dine. De røde prikkene kan brukes til å rotere de tre delene, og de blå prikkene brukes til å flytte dem. Hvis du vil speilvende den rosa biten, kan du klikke på den.
Starthjelp
- Bruk et speil for å sjekke symmetriene.
- Prøv å holde den største biten i en fast posisjon. Så kan du plassere rektanglet i alle mulige posisjoner, og til slutt plassere det lille kvadratet slik at du får en symmetrisk figur.
Løsning
|
|
|
|
|
|
|
|
|
|
|
|
Lærerveiledning
Hvorfor arbeide med denne oppgaven?
Denne oppgaven hjelper elevene til å tenke over symmetrier i mange ulike figurer. Det er en oppgave der det går raskt å se om en løsning er riktig. Den har utfordringer som kan engasjere en hel klasse, og som gir rom for mange valg og kreativitet. Elevene må samarbeide og ta ansvar for å sjekke hverandres arbeid, for det er umulig for læreren å være forberedt på alle de mulige kombinasjonene i figurer som kan dukke opp.
Mulig tilnærming
Disse kopioriginalene kan være nyttige:
Oppgaven finner du her.
Bilde av figurene i oppgaven som kan klippes ut, finner du her.
Når elevene kommer til timen, får de utdelt kopier av de tre delene på stivt papir, eller de får arbeide med appleten som ligger i aktiviteten. Be klassen om å sette sammen formene til en symmetrisk figur. Samle klassen etter en liten stund, og hør hva de har funnet. Gjør de riktige løsningene synlige på tavla, slik at alle har oversikt over løsningene som alle er enige om.
La elevene arbeide videre med å finne flere løsninger, alene eller i par. Etter en stund kan de inviteres til å tegne flere løsninger på tavla. Hvis de har funnet for eksempel seks ulike figurer, kan du foreslå at dette settet med tre figurer kalles «6-løsningssett».
«Nå er det tid for å ‘slå dette problemet’. Tegn deres egne former slik som dem i oppgaven. De er satt sammen av kvadrater i et kvadratisk rutenett der det samlede arealet er 10. Kan dere finne tre figurer som gir flere symmetriske løsninger enn figurene vi begynte med? Vi leter etter et ‘7-løsningssett’, et ‘8-løsningssett’ osv.» (Hvis klassen har funnet flere enn seks løsninger på den opprinnelige oppgaven, blir utfordringen med å finne sett av figurer som har flere løsninger, enda større!)
«Kan vi til sammen i klassen finne et ‘0-løsningssett’, et ‘1-løsningssett’, et ‘2-løsningssett’, et ‘3-løsningssett’ osv.?»
«Når dere har designet et sett og tror dere har funnet alle mulige måter å lage symmetriske figurer av dem på, kan dere tegne dem tydelig og lime arket opp på tavla, slik at alle kan sjekke.»
Gjør tavla klar med overskrifter: «0-løsningssett», «1-løsningssett», «2-løsningssett», «3-løsningssett» osv. Be alle om å sjekke minst én av de andres løsning for å bekrefte at den er plassert i riktig kategori.
Sørg for å ta vare på alle resultatene fra økta, slik at det kan brukes i arbeidet videre. Dette er et arbeid som kan strekke seg over litt tid.
Gode veiledningsspørsmål
- Hvor kan speilingslinjene ligge?
- Finnes det en systematisk måte for å sjekke at du har funnet alle mulige løsninger?
Mulig utvidelse
Elevene kan ha nytte av å studere denne løsningen som viser hvordan en elev har arbeidet systematisk med å lete etter løsninger. Prøv å finne ut hvordan eleven har tenkt. (Det mangler én løsning i dette settet – du finner den under Løsning)
Oppmuntre elevene til å finne tre figurer som har svært få (eller ingen) mulige symmetriske sammensetninger, og/eller figurer som har flere løsninger enn de som er funnet så langt.
Mulig støtte
Ha speil og sakser tilgjengelig slik at elevene kan klippe ut, speile og brette figurene for å kontrollere om de har symmetrilinjer.
Ressursen er utviklet av NRICH