L-triominoer
Aktivitet
En triomino er en figur som er satt sammen av tre kvadrater. En L-triomino har form som en L.
Dette er en L-triomino i størrelse 1:
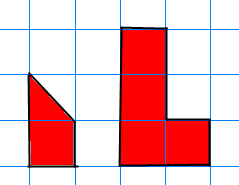
Dette er en L-triomino i størrelse 2:
Den kan settes sammen av fire L-triominoer i størrelse 1:
Hvordan kan du sette sammen en L-triomino i størrelse 4 ved å bruke bare L-triominoer i størrelse 1? Tenk over hvordan sammensetningen av triominoen i størrelse 2 ovenfor kan være til hjelp.
Formuler et overbevisende argument for hvordan du kan tessellere (fylle uten hull eller overlapping) L-triominoer av størrelse 8, 16, 32, …, 2n med L-triominoer av størrelse 1.
Hvor mange L-triominoer av størrelse 1 trenger du for å lage størrelse 8, 16, 32, …, 2n?
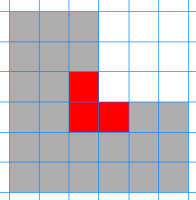
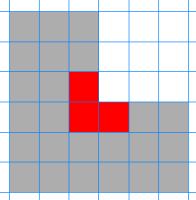
Hva med L-triominoer med oddetallstørrelse? Figuren nedenfor viser arealet av en L-triomino i størrelse 3 som skal fylles av L-triominoer i størrelse 1.
Kan du finne en enkel måte å fylle denne på ved hjelp av de to «brikkene» nedenfor?
Kan du finne en måte å bruke ideene fra L-triomino i størrelse 3 til å sette sammen en L-triomino i størrelse 5, og deretter i størrelse 7, 9, 11 …?
Få et hint
Formuler et overbevisende argument for hvordan du kan tessellere alle L-triominoer med oddetallstørrelse ved hjelp av L-triominoer i størrelse 1.
Kombiner ideene dine, og formuler et overbevisende argument for at det er mulig å tessellere L-triominoer i enhver størrelse med L-triominoer i størrelse 1.
Her er et interaktivt rutenett hvor du kan prøve ut ideene dine.
Starthjelp
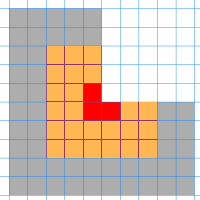
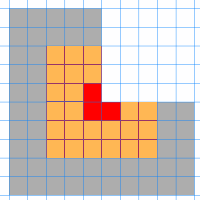
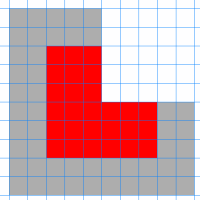
Studer figuren nedenfor. Den viser L-triominoer i tre ulike oddetallstørrelser.
Kan du finne en måte å tessellere L-triominoer i størrelse 1 på rundt den røde, slik at det oransje feltet fylles? Og kan du finne en måte å tessellere på rundt det oransje, slik at det grå fylles?
Kan du utvide figuren til størrelse 7 og fylle den opp? Og deretter til størrelse 9?
Løsning
Du kan bygge en L-triomino i størrelse 2 ved å bruke 4 L-triominoer i størrelse 1.
Du kan bygge en L-triomino i størrelse 4 = 22 ved å bruke 4 L-triominoer i størrelse 2. Da bruker du 42 = 16 brikker i størrelse 1.
Du kan bygge en L-triomino i størrelse 8 = 23 ved å bruke 4 L-triominoer i størrelse 4, da bruker du 43 = 64 brikker i størrelse 1.
For å sette sammen en L-triomino i størrelse 2n trenger du 4n brikker i størrelse 1. Hvis du skal sette sammen en L-triomino i størrelse 2n, kan du alltid dele den opp i fire L-triominoer i størrelse 2n – 1.
En L-triomino i størrelse 3 kan settes sammen av én i størrelse 1, én i størrelse 2 og to rektangler satt sammen av to i størrelse 1 «i hver ende».
Når du vil lage en L-triomino i størrelse 5, begynner du med størrelse 3, så setter du en i størrelse 2 i hjørnet og fyller opp med rektangler.
For å sette sammen L-triominoer i størrelse 7, 9, 11 osv. begynner du med en i størrelse 5, setter en i størrelse 2 i hjørnet og fyller opp med rektangler.
Generelt
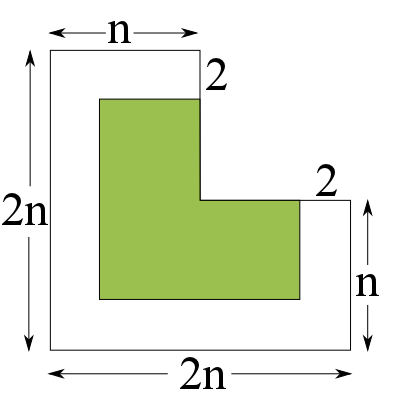
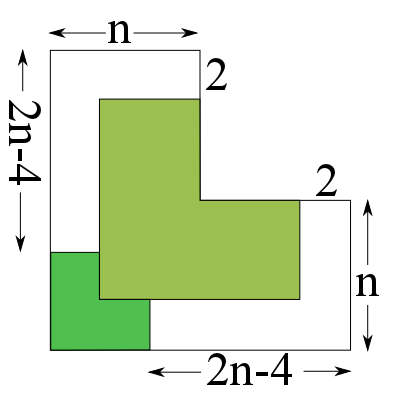
La n være et oddetall, og anta at vi kan sette sammen en L-triomino i størrelse (n – 2) – den grønne delen av figuren under. Så fyller vi opp med en L-triomino i størrelse 2 i hjørnet:
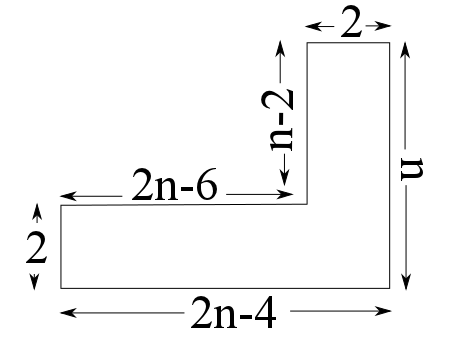
Nå står det igjen å vise at vi kan fylle to arealer med følgende form:
1. Hvis n er en multippel av 3 (dvs. hvis n er et tall i 3-gangen), vil det høyre rektanglet med areal 2 x n kunne fylles med 2 x 3-rektangler. Da står det igjen et rektangel med areal 2 x (2n – 6). 2n er et tall i 3-gangen, så dette arealet kan også fylles av 2 x 3-rektangler.
2. Hvis n får 1 til rest ved divisjon med 3 (dvs. n = 3k – 2), kan vi fylle hjørnet nede til venstre med en L-triomino i størrelse 2. Så må vi fylle to rektangler med areal henholdsvis 2 x (2n – 8) og 2 x (n – 4). Her vil (n – 1) være et tall i 3-gangen, og vi kan skrive de to arealene som 2 x (2(n – 1) – 6) og 2 x ((n – 1) – 3). Begge arealene er altså 2 x (en multippel av 3), og kan dermed fylles av 2 x 3-rektangler.
3. Hvis n får 2 til rest ved divisjon med 3 (dvs. n = 3k – 1), vil (n – 2) være en multippel av 3, og det samme blir (2n – 4). Da kan vi fylle rektangelet nederst, 2 x (2n – 4) med 2 x 3-rektangler. Vi står igjen med et rektangel med areal 2 x (n – 2), og det kan også fylles med 2 x 3-rektangler.
Dette viser at vi kan tessellere en L-triomino av en hvilken som helst størrelse med L-triominoer i størrelse 1, for ethvert helt tall er enten på formen 3k, 3k – 1 eller på formen 3k – 2.
Lærerveiledning
Hvorfor arbeide med denne oppgaven?
Dette problemet begynner med noen enkle oppgaver rundt tessellering og forstørring av figurer. Det viser elevene hvordan et bevis kan bygges opp trinn for trinn ved å bryte det opp i spesialtilfeller. De får dessuten se hvordan vi kan utnytte den muligheten at større former kan lages ved å gjenta mindre former som vi allerede har laget, altså at et steg i ett resonnement bygger på det foregående.
Mulig tilnærming
Begynn med å vise elevene den minste L-triominoen, og utfordre dem til å bruke denne formen til å fylle L-triominoer i størrelse 2, 3 og 4. La dem bruke ruteark. De kan komme til å arbeide nokså usystematisk til å begynne med, og kanskje klarer de ikke å fullføre alle figurene. Etter litt tid til å prøve seg fram kan dere snakke sammen i klassen om hvor mange brikker som trengs til hver av figurene. Dere kan også snakke om ideen med å forstørre figurer som allerede er etablert.
Så snart alle har fått til å fylle ut de første få L-triominoene, og dere har fått opp løsninger på tavla slik at alle kan se dem, kan arbeidet følges opp:
«Jeg lurer på om alle størrelser av L-triominoer kan tesselleres.»
Oppmuntre elevene til å arbeide systematisk, slik at de gradvis bygger opp forståelse av hvordan de ulike størrelsene kan fylles opp. Be dem tenke over hvordan de kan bruke løsningen av størrelse 2 til å fylle størrelse 4. Kan de utvikle denne ideen videre og komme fram til en overbevisende forklaring på hvordan en L-triomino i størrelse 2n kan fylles? Samle klassen til en samtale der de kan dele det de har kommet fram til så langt.
Så kan du introdusere L-triominoer med oddetallstørrelser. Vis disse to figurene for klassen:
Utfordre elevene til å finne enkle måter å utvide løsningene på, fra ett oddetall til det neste. Det skal lede til et argument for at alle oddetalls L-triominoer kan tesselleres.
Til slutt må elevene tenke over hvordan de to argumentene kan kombineres for å bevise at alle L-triominoer kan tesselleres. Det er en fin anledning til å diskutere de formelle stegene i et matematisk argument.
Gode veiledningsspørsmål
• Hvordan kan jeg bruke det jeg vet om å tessellere en L-triomino i størrelse 2, til å tessellere en i størrelse 4?
• Hvordan kan jeg bruke det jeg vet om å tessellere en L-triomino i størrelse 3, til å tessellere en i størrelse 5?
• Hvordan kan jeg bruke det jeg vet om å tessellere L-triominoer i oddetallstørrelser og i størrelse 2n, til å vise at jeg kan tessellere L-triominoer i alle størrelser?
Mulig utvidelse
Undersøk tessellering med disse formene (brikkene) som utgangspunkt:
Bevis at alle størrelser av L-triominoer kan tesselleres.
Mulig støtte
En måte som kan gjøre det enklere å løse problemet med L-triominoer i størrelse 2n på, er å tegne fire i størrelse 2 på ruteark, klippe dem ut og sette dem sammen til størrelse 4. Om en vil, kan en tegne fire i størrelse 4 på ruteark, klippe dem ut og sette dem sammen til størrelse 8, osv.
Ressursen er utviklet av NRICH